Introduction
The SARS-CoV-2 virus pandemic, commonly called COVID-19, led countries worldwide to enforce social restrictions to avoid the coronavirus spread. The most common contingency measures, taken by multiple governments, is to limit the citizens traveling, as well as social interactions that occur between them. The previous described measure is commonly known as “social distancing” and has the purpose to limit as much as possible the exchange of segregations between people’s interaction which is the main event that leads to the exponential growth of the COVID-19 propagation. [1]
However, there are scenarios in which multiple pedestrians spend daily hours walking into multiple agglomerations, where the social distancing measure is not present. In 2019, the Universidad de Los Andes reported around 14 thousand undergraduate students, 3.000 master’s students, and about 364 doctoral students. [2] in a campus area that covers around 11.4 hectares [3]. As it is observed, the university institution has a large volume of pedestrians circulating daily through the different facilities of the campus (multiple corridors and interconnection building routes). This scenario was the common behavior before the implementation of virtual classes by the institution due to the pandemic. Therefore, given the importance to implement the social distancing measure within the campus considering students agglomerations, we proceed to propose a mathematical model to minimize a student exposure from a COVID-19 contagion with also taking into account the shortest distance criteria to be traveled between the two places that a student has to travel across the university campus.
The mathematical model was designed based on the characteristic of the solution, which is the modeling of two main objectives based on the problems criteria to be minimized: traveling distance and COVID-19 contagion risk between two points on the university campus. Therefore, the developed mathematical model was designed for a bi-objective optimization. However, based on the student pedestrian mobility patterns modeled for the corresponding cost parameters related to the traveling distance criteria, the model converged into a mono-objective optimization, given the fact that the modeling resulting into the two main criteria overlapping each other in their optimal solutions. Therefore, the approached heuristic - which was chosen to be the Dijkstra algorithm (as it corresponds to a shortest cost path exact heuristic) - only solve one of the two main criteria in each executed scenario. Consecutively, the heuristic was validated with the modeled bi-objective mathematical model given a set of scenarios that took into account the criteria to be minimized and a particular source and destiny university building, day and schedule. Finally, the heuristic is proposed to be executed and used through a mobile application, where a student pedestrian determines a route to travel the campus in which the contagion risk is minimized at a certain time.
Additionally, for readers context, it should be noted that the presented research is an extended version of the published version made on the 2021 International Conference on Applied Informatics [4]. This extended version provides more details related to the mathematical model parameters set up -such as data processing, pedestrian traffic displacement pattern and hierarchy data persistence used for the modeling - and general overview and future work section.
The research content is structured as follows: Section 2 describes related works, and the identification and relevance of the problem to be solved. Section 3 describes the overall solution design processes made for the final product, which are the definition of the mathematical model and the problems functions modeling (which are the distance to be travel and the contagion risk). Section 4 shows the model design process of the multi-objective mathematical optimization with the descriptions and justifications developed for the implementation of the mobile application. Section 5 describes the modeling and in-depth description of the problem modeled in the phases presented in Section 4. Additionally, the section describes the development and validation of the solution algorithm. Section 6 shows the mobile application design and development that corresponds to the user-facing solution. Section 7 describes the final results obtained by our work. Section 8 describes the performance results obtained in the initial iteration of the project, enunciating the main limitations and therefore improvements to be made to the initial iteration. Finally, Section 9 describes the main tasks and features that have been identified in this research to be done - in order to improve software performance and COVID-19 risk contagion modeling - as a second iteration of the project.
Related Work
The following studies emphasized how mobility events are related to the spread of the SARS-CoV-2 virus. The same COVID-19 susceptibility probability equation for an individual in pedestrian congestion was used through these related works. These studies describe simulations to represent the pedestrian mobility patterns under different types of events in a common day.
In [5], researchers performed simulations of human mobility models to study the dynamics of coronavirus infection in order to get a dynamic model of the virus spread. To obtain the nature of the epidemiological dynamics, the study made use of the SIR (Susceptible, Infected and Recovered) model. Through contagion rates planned in the model, the behavior of different groups populations was simulated. If a susceptible person and an infected person meet, there is a probability that the susceptible person will become infected. Time after infection,the person typically recovers. Therefore, the study introduced a contact graph constructed from everyday situations such as agglomerations in public trans-port, work, home, and others (scenarios in which the SIR model could be applied and studied). Finally, after executing the simulations of the contact graph with the epidemiological dynamics previously stated, the study set out strategies as conclusions, such as the suspension of public transport, total quarantine, and others social decisions, in order to prevent and reduce the spread of the virus.
For instance, one of the researched works created an epidemiological model based on agents (called PanCitySim) in which the movement of many individuals were modeled in a city. For this purpose, the model used a graph to represent the contact of many activities performed by the population in the whole city. In this sense, the spatio-temporal properties of an epidemic were studied according to the SIR model in order to represent the impact of human interactions to the transmission of the virus [6].
Thus, it was feasible to study human mobility models in cities in order to understand the COVID-19 spreading behavior. Based on these related works, a solution could be applied to the mobility patterns associated with pedestrians and their environment within the Universidad de Los Andes, as well as mathematical models and probabilities associated with the spreading of the coronavirus.
Additionally, as the date of the research development, there was no evidence of work of the COVID-19 contagion risk optimization applied to a specific pedestrian traffic scenario, and therefore, an optimal solution application that a user could use during their traveling (based on a scenario where the users faces pedestrian agglomerations that increase the coronavirus contagion probability). Hence, based on the existing human mobility models simulations, we find the opportunity to use as base the epidemiological models to optimize pedestrian traffic from a concrete scenario and related data, and also to expose the solution through a software tool that could be used in real-time.
General Solution Design
The design process established for the solution implementation is described below. Figure 1 shows a diagram of the main activities developed in the process, as well as the tools, investigations and results associated with each activity. In the diagram each box (white) has the statement of each activity written, where their entries (green) and the respective software tool (blue) or associated research (yellow) are shown. The upper left numbers represent the sequence step when the activity was develop. Finally, the results or outputs of each activity (red) and the arrows indicate the dependencies between activities and inputs.
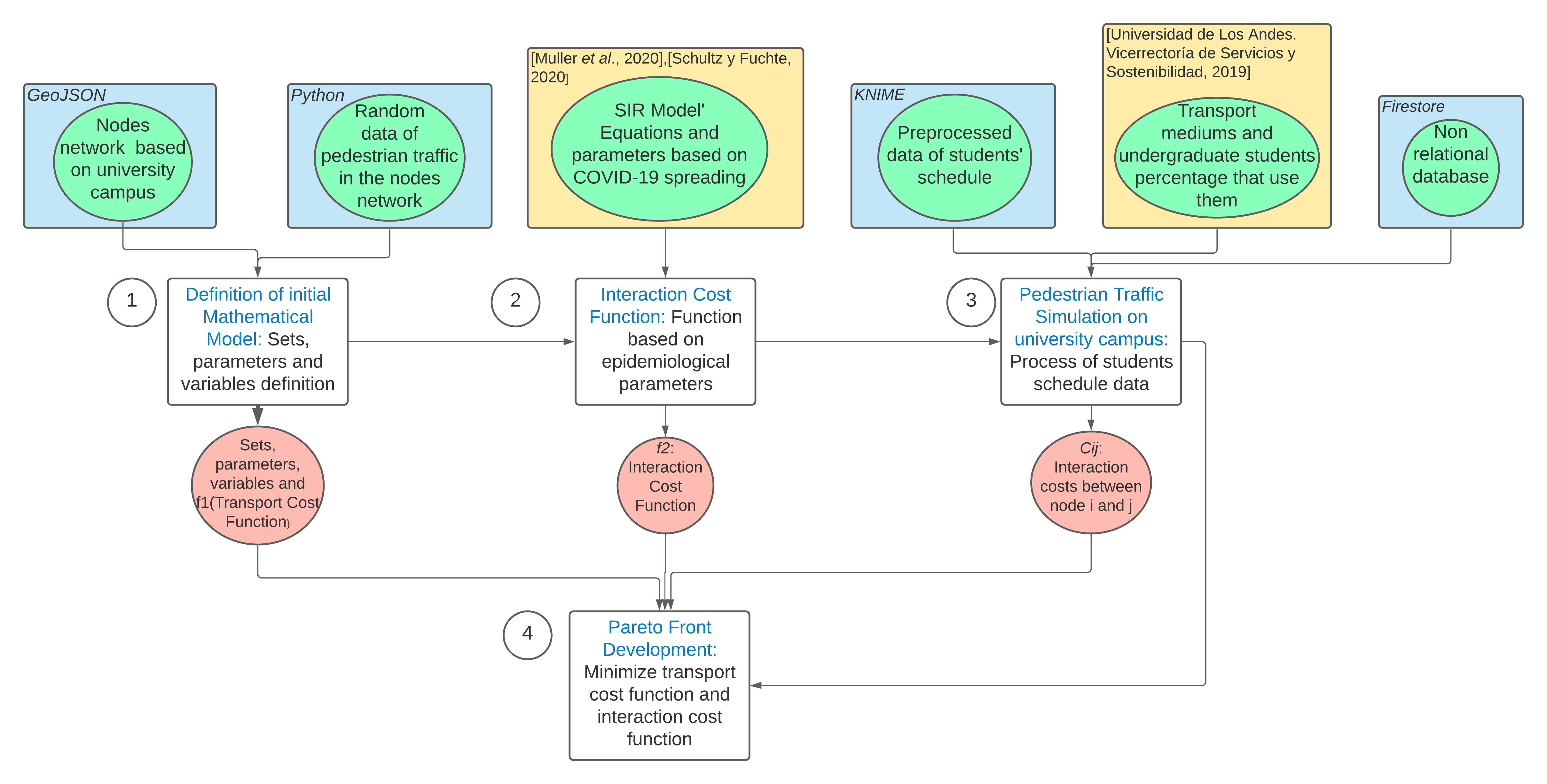
As a reference for details of each main activity, Section 4 describes the detail of the activities Definition of initial Mathematical Model, Interaction Cost Function, Pedestrian Traffic Simulation on university campus and Pareto Front Development.
Following is an general overview of the inputs, outputs and the description of each main activity
Definition of initial Mathematical Model
First, it was modeled through the GeoJSON website an graph by plotting points on the university map where there was any routes across the university campus.
Then, based on a dataset with anonymous student data related to the classes schedule that the students have, it was generated random pedestrian based on the potential nodes that a student has to travel in order to attend to their buildings’ classes. The mobility patterns and the loading of the pedestrian traffic was implemented through Python scripts and libraries.
Finally, as activity output, we developed the design and modeling of \(f_{1}\) function, which is the function that represents the distance (measured in units) between each pair of nodes that have a link on the university. The modeling activity includes a sets, parameters and variables definition for the \(f_{1}\) function.
Interaction Cost Function
For the construction of the \(f_{2}\) function, with is the function that represents the COVID-19 probability risk contagion between each pair of nodes that have a link on the university, we used the proposed equation in [5], which models the susceptibility probability of contracting the coronavirus based on the numbers and characteristics of the social encounters that people have during their displacements.
Pedestrian Traffic Simulation on university campus
Based the culmination of the two previous activities, it was proceeded to model the student pedestrian traffic, which assign the respective costs to \(f_{1}\) and \(f_{2}\) on each link of each pair of nodes that have a connection on the university graph.
As inputs, we considered the pre-processed data of the student classes schedule dataset (which was done through the software tool KNIME) to generate mobility patterns and displacement that students would have and consecutively the assignation of the social encounters (costs for the interaction cost function) between each existing link on the university graph. The interaction costs between each pair of nodes with connection was denoted as \(C_{ij}\), where it is represented the amount of students a student would encounter when traveling from node \(i\) to node \(j\)
Also, to determine the initial nodes where students would began their displacement, we took the [7] as a reference where the students would enter to the university in terms of medium transport arrival nodes.
Finally, we decided to store all the loaded students mobility patterns data on the Firebase’ Firestore non-relational database, which allows to store more efficient this type of data based on the hierarchy presented (student pedestrian traffic based on a academic cycle, a day and a certain schedule).
Pareto Front Development
Based on the setup of the two functions (distance and interaction costs functions), we implemented a Pareto Front taking into account the modeled functions.
Multi-Objective Mathematical Optimization Model
We establish a mathematical model to minimize the distance traveled by a student and the COVID-19 contagion risk when facing others students during the displacement. Therefore, the mathematical model included a transportation cost matrix represented as the distances between each pair of nodes included in the route of the map to travel. Likewise, an interaction costs matrix was also established, where it is represented the student pedestrian traffic through the nodes in the university campus map. Additionally, in the mathematical model we defined a minimum coverage radius for each node, which is the maximum distance that must be for each pair of nodes to be a connection.
We define the initial nodes network using GeoJSON web tool [8], where graph nodes were placed consecutively on each existing university campus path. Once the coordinates of the different nodes had been exported in a file in JSON format, they were loaded as parameters to the mathematical model. For the mathematical model, sets, variables, and parameters understanding, see Table 1.
| Category | Symbol | Description |
|---|---|---|
| Sets | \(N\) | Number of nodes in the network |
| Parameters | \(Ci_{ij}\) | Interaction cost between node \(i\) and node \(j\), which is the number |
| of people that walk through the link (i,j). | ||
| \(Ct_{ij}\) | Transport cost between node \(i\) and node \(j\), which is the euclidean | |
| distance between these nodes | ||
| \(S\) | Source node number, in which a student started its walk | |
| \(D\) | Destination node number, in which a student finished its walk | |
| \(RC\) | Node’s Ratio Coverage, which is the maximum distance that two | |
| pairs of nodes must have to exist a connection link between them. | ||
| Variables | \(X_{ij}\) | Binary decision variable that shows whether the student chooses |
| the link between node \(i\) and node \(j\) as a part of its path. | ||
| from the source node to the destination node. 0 if otherwise. |
Hence, to validate the proposed model, the following objective function was defined:
Minimize
\[\sum_{i \epsilon N} \sum_{j \epsilon N} X_{ij} \cdot (Ct_{ij} + Ci_{ij})\]
Subject to: \[\sum_{j \epsilon N} X_{ij} = 1 \hspace{35pt} \forall i \epsilon N | i = S\]
\[\sum_{j \epsilon N} X_{ij} = 0 \hspace{35pt} \forall i \epsilon N | i = S\]
\[\sum_{i \epsilon N} X_{ij} = 1 \hspace{35pt} \forall j \epsilon N | i = D\]
\[\sum_{i \epsilon N} X_{ij} = 0 \hspace{35pt} \forall j \epsilon N | i = D\]
\[\sum_{j \epsilon N} X_{ij} - \sum_{j \epsilon N} X_{ji} = 0 \hspace{35pt} \forall i \epsilon N | i \neq D \land i \neq S\]
\[X_{ij} \cdot Ct_{ij} \leq RC \hspace{35pt} \forall i,j \epsilon N\]
The objective function of the mathematical model is subjected to the constraints represented in Equation [2] to Equation [6]. In Equation [2] it is indicated that the source node should only have one outflow, which dictates that a student can only take one path from its origin node. Equation [3] ensures that a student cannot returned to its source node. Equation [4] ensures that the student reaches its destination node. Equation [5] establishes that once a student arrives to the destination node, he cannot travel to other paths or nodes. For intermediate nodes between the source node and the destination node, Equation [6] establishes that if a student reaches an intermediate node, he/she has to leave that node. Finally, to guarantee that the model chooses links within the ratio coverage of each node, Equation [7] was proposed. For the mathematical model implementation, we executed the model on the Pyomo optimization framework on an Intel Core i5-6200U, 2.3 GHz, 7.7 GiB system.
Interaction Cost Function
The susceptibility probability of contagion proposed by [5] was used in our work, which can be observed in Equation [7].
\[P_{n, t} = 1 - e ^ {- \theta \cdot \sum_{m \epsilon M} q_{m, t} \cdot i_{nm, t} \cdot t_{nm, t}} \label {eqn: 7}\]
Where \(M\) is the set of students with whom a student was in close contact, with the following variables and parameters: \(P_{n, t}\) is the probability of a student \(n\) to receive an infectious dose. However, as stated in [9], this probability should not be understood as “probability of contracting the virus”, since this depends on the immune system of each student. \(\theta\) is the calibration factor for a particular disease. \(q_{nm, t}\) corresponds to the microbial load between two people, which is the amount of virus that the student \(m\) transmits in time \(t\). \(i_{nm, t}\) is the contact intensity between the person \(n\) and \(m\), which corresponds to the distance. Finally, \(t_{nm, t}\) represents the time that a student \(n\) interacts with a student \(m\) during an interval \(t\).
For the simplicity of the proposed mathematical model, we assumed that the distance between each pedestrian and each user corresponds to 1 meter and that their interaction time was 0.5 seconds. However, due to the fact that as of the date this research was developed, no calibration parameters and microbial load of COVID-19 were known. Thus, parameters estimated by the previously mentioned studies were used.
First, the value \(q_{m, t}\) was assigned as 1 based on estimates made by [5]. Similarly, the calibration parameter \(\theta\) was taken as \(\frac {1}{20}\) based on studies conducted by [9] in closed spaces such as aircraft interiors during commercial flights.
We considered that the choice of this calibration value should be made on the assumption that all routes in the campus rely on indoors spaces (which is the assumption of a pessimistic scenario). With this decision, it was possible to establish an equal load of micro-organisms in the environment for all the connections between nodes, which allowed the model to calculate the best path based on the segregations caused by other students and not on the dispersion caused by other external factors.
Pedestrian Traffic Simulation on the university campus
Data preprocessing
To establish the parameters linked to the interaction cost of the model, students pedestrian traffic was simulated in a post-COVID-19 scenario, which is a scenario in which the traffic of students within the university campus is not affected by the current pandemic at the date of publishing this research. For this reason, the anonymized schedules of undergraduate students in the first semester of 2019 dataset was processed, as well as the semester current academic schedule.
Then, the data was pre-processed and cleaned through the data analysis software KNIME [10].
Using this tool, the list of courses was matched to the courses registered by the students. The operations performed on the data set are presented below:
Registered courses that did not have a classroom attribute were deleted. Since these courses had virtual modality, the students enrolled in those courses did not generate pedestrian traffic.
Registered courses that did not have a record of start or end time were deleted. Without having a specific range of time the traffic generated by students in a period of time on a given day is not known.
Courses attribute values such as Space and Availability were deleted, as they were not significant for the pedestrian traffic simulation.
For simplicity of the database entries, the secondary classrooms of the enrolled courses were eliminated, taking as pedestrian traffic the displacement towards the primary classrooms of their registered courses.
The rows that contained rooms outside the Main Campus (i.e. Practice Center) were eliminated since the network of nodes to be modeled only have into account buildings that are located within the main campus of the university.
Finally, the result was a dataset that had the following attributes with a total of \(65,536\) records. The final courses attributes are shown in Table 2 with their respective description.
| Data field name (written in Spanish) | Description |
|---|---|
ID |
Student ID. |
NRC |
Course ID. |
MATERIA |
Department or Faculty of the course. |
NOMBRECURSO |
Name of the course. |
PARTE |
Current academic cycle of the course. |
SALON1 |
Building where the course was taught. |
HINI1 |
Time and minutes when the course started. |
FINI1 |
Time and minutes when course ended. |
L,M,I,J,V,S |
Days on which the course was taught. |
Configuration and loading of pedestrians’ initial and intermediate nodes
Once the final dataset to be used as parameters in the model was obtained, the students pedestrian traffic data was loaded into a non-relational database.
For this task, a Firestore database was created on the platform Firebase [11], and for the loading data process, scripts written in Python programming language were used [12].
Then, each dataset record was uploaded as the origin and destination buildings that each student has in a change of classes in an academic cycle, day and specific time. The following describes how special cases were handled when the record consisted of the first class of the day, or when a student had two or more non-consecutive classes on the same day:
For a student’s first class of the day, it was decided that a student would arrive at the university campus through the transport nodes identified in Uniandina Mobility Survey (Encuesta de Movilidad Uniandina) carried out in May 2019 [7] , where each means of transport has an associated percentage, which represents the percentage of students that travels on the respective means of transport.
Then, a random variable that oscillated within the ranges of percentages was defined, and from that variable value, it was assigned within the closest mean of transport percentage.
Likewise, the network nodes equivalent to where the transportation stops are located within the university campus were defined. Modes of transportation such as Hike were omitted, since it does not exist or is not known with certainty. Also it was considered that students can arrive from multiple points in the network using this type of modes.
For non-consecutive classes belonging to the same day, it was decided to define random nodes where students would spend their free hours. The choice of these nodes was made arbitrarily. The set of nodes assigned in free hours consisted of the Prado El Bobo, Cafeteria Central and Biblioteca Ramón de Zubiría (these places are part of the university campus).
Once the data had been uploaded to the database, a hierarchical non-relational database was obtained based on the academic year, day, and class change schedule. In Figure 2 you can see a diagram of the database schema.
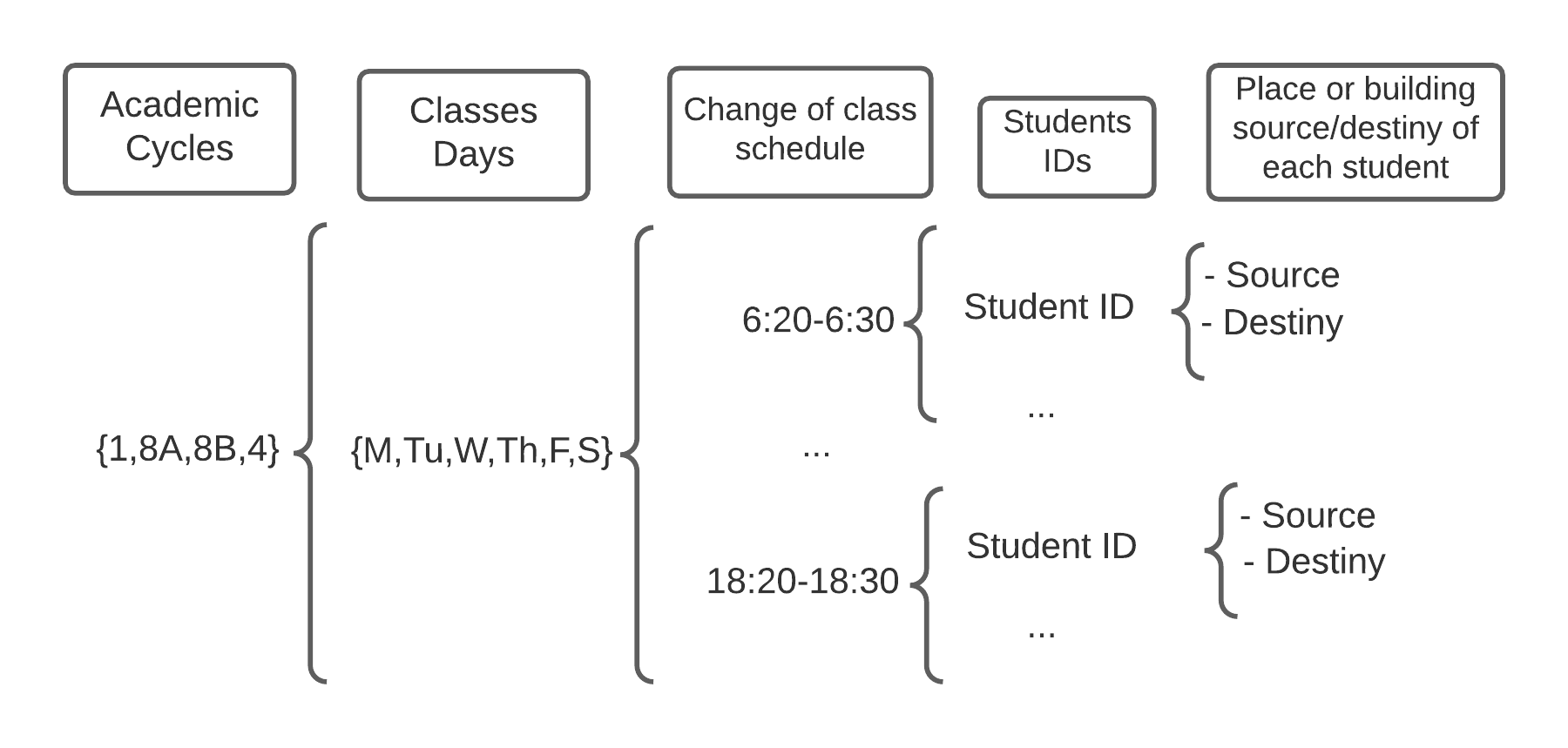
For the structure hierarchy of the database, it was composed from top to bottom as follows:
Academic cycles: Semester period when the classes are taught. This allows to characterize the student pedestrian traffic based on the current period. The selection of a particular academic cycles helps to filter pedestrian congestion peaks based on a certain period of time. Examples of academic cycles values includes first and last 8 semester week (8A and 8B respectively).
Classes Days: Laboral weekdays. This allows to segregate pedestrian traffic based on the classes days that students have. Laboral weekdays go from Monday to Saturday.
Change of class schedule: Intervals between classes which are the times where student make their displacements from the source node (which could be transport medium node or a building node where they were having a previous class) to their new destiny node. The modeling of this interval is dictated by how the university schedules the intervals of the courses. The rule is applied in general for all classes scheduled in the university, where all classes start at o’clock or half hour pass o’clock, and end 10 minutes before those times. Intervals go from the first interval for the first class of the day (6:30 a.m.) to the last class taught on a day (6:30 p.m.)
Student ID: Student dataset identification. Students contained in the change of classes interval set, where it is indicated that a student would displace during said interval.
Source/destiny place or building of each student: Source and destiny name where the student will travel across the university campus. With the source/destiny of multiple pedestrians as the last bottom level, pedestrians data could be effectively loaded to the parameters of the interaction costs of the mathematical model and heuristic, as it only takes for parameters the source and destiny of a list of multiple student pedestrians.
Pedestrian traffic’ displacement pattern
For modeling the route pattern that each student was going to travel when moving around the campus, we decided that for the simulation the students would seek for the shortest way to displace from their source building to their destination building.
For this task, it was assumed that each student would move through their route nodes using the Dijkstra Algorithm for minimal cost path (taking the distance between each pair of nodes as the cost) [13].
Consequently, the selection of each path by each student set the interaction costs of the mathematical model and the solution heuristic - which is described in depth in Section 5 -. At Table 3 is the terminology used for Algorithm 1, which was used to model the pedestrian traffic parameters to the interaction cost variable.
As a general description of the algorithm, the algorithm seeks to assign to every student the set of links that the student would travel as a mobility pattern for going from their source node to their destiny node, and consecutively assign for each link that the student will travel the aggregated interaction cost for that link in a global variable. In the algorithm’s first loop, it is assign the optimal set of links (given by Dijkstra algorithm) that each student in the pedestrian traffic will take. Then, in the second loop it is checked for all pair of links in the university graph if the link is associated with a link choose by the Dijkstra algorithm for a students’ path, then the counter of the number of students traveling through that link is increased (which is the interaction cost related to that specific link).
| Symbol | Description | Assumptions |
|---|---|---|
| \(N\) | Set of network nodes. | |
| \(E\) | Set of students that displace in a specific academic cycle, day and schedule. | |
| \(S(i)\) | Student source node \(i\). | \(\forall i \epsilon E \hspace{10pt} \forall S(i) \epsilon N\) |
| \(D(i)\) | Student destiny node \(i\). | \(\forall i \epsilon E \hspace{10pt} \forall D(i) \epsilon N\) |
| \(Sp(i)\) | Optimal set of links that a student \(i\) has to take to displace from \(S(i)\) to \(D(i)\). | \(\forall i \epsilon E \hspace{10pt} \forall S(i),D(i) \epsilon N\) |
| \(D_{ij}\) | Optimal links calculated by Dijkstra Algorithm from node \(i\) to node \(j\) displacement. | \(\forall i,j \epsilon N\) |
| \(C_{ij}\) | Interaction cost, which the amount of pedestrian from node \(i\) to node \(j\) during a certain period of time. | \(\forall i,j \epsilon N\) |

Pareto Front Development
Consecutively, we implemented a Pareto Front to observe the behavior of the transport and the interaction cost functions when they are minimized and one function has more weight over the other.
Therefore, the Pareto Front was executed through the method \(\varepsilon\) -constraint [14]. For this calculation, the previously defined network of nodes was used and the parameters of the transport function were assigned based on the traffic loaded in the database.
Finally, we defined a weights vector in which each vector’ element multiply each function on each iteration, in order to give greater weight to one function compared to the other. The mathematical expression was defined:
\[W = {[10,20, \dots, 50]}\]
where for each element of \(W\) would represent the upper limit that \(f_ {2}\) should have when wanting to minimize \(f_ {2}\) (this is reflected in the additional restriction described below). Therefore, each element \(W\) was iterated to obtain values close to the limit of \(f_ {2}\). It should be noted that the mathematical model of the method also includes the restrictions initially set in the Section 4.
The Pareto Front execution was computed on an Intel Core i5-6200U, 2.3 GHz, 7.7 GiB.
For Each \(w \epsilon W\):
\[f_{1} = \sum_ {i \epsilon N} \sum_{j \epsilon N} X_{ij} \cdot Cij\]
\[f_{2} = \sum_ {i \epsilon N} \sum_{j \epsilon N} X_{ij} \cdot Cij\]
Minimize \[f_ {1}\]
Subject to: \[f_{2} \leq w\]
See Equation [2] - Equation [7]
Heuristic
As the research problem can be represented as a minimum cost problem, where for each node’s link exists two types of cost - transport cost and interaction cost - we used a known heuristic to solve the minimum cost problem by combining in a same scale the two types of cost for each link. The Dijkstra Algorithm [13] was used as a solution algorithm, where the student through the developed mobile application can choose the criterion to minimize given a set of parameters.
Regarding the costs unification, the costs for each link were normalized, and then multiplied by a weight represented by a scalar between 1 and 0. Finally, the product of the normalized costs and their scalar was added, resulting in a single cost matrix. It should be noted that the scalar weight is the representation of the path criterion selected by the user (i.e. 0 as least importance, 1 as greatest importance).
However, we found that given the modeling of pedestrian traffic described in the Section 4.2 and the obtained Pareto Front results in different scenarios, the problem of minimization of the transport cost function and the interaction cost function only had solutions in the limits of each function, which is a solution was not found that minimized the two objectives "as equal", but rather two optimal solutions were obtained that minimize only one function.
Bi-objective problem understanding
To understand the reason for the existence of only two optimal solutions for the minimization problem of \(f_{1}\) and \(f_{2}\) (as conventions, \(f_{1}\) is referred as the transportation cost function and \(f_{2}\) is referred as the interaction cost function.), it must be remembered how the distribution of traffic was defined in the Section 4.2, which was done under the assumption that every student who travel through the campus would choose the shortest route in the network of nodes.
Scenarios were obtained where all the costs associated with \(f_{2}\) are distributed by the links that minimize \(f_{1}\). Therefore, when it is desired to minimize only \(f_ {1}\), links are obtained when it is desired to maximize \(f_{2}\). Similarly, when only \(f_{2}\) is minimized, the chosen links have no costs for this function. Those links, since they are not optimal for \(f_{1}\), maximize the value of said function.
To describe the understanding of the problem in more detail, see Figure 3. In the diagram case, it it observed that in each optimal link chosen by Dijkstra’s Algorithm (colored with blue and where \(d \epsilon D\)) between a source (colored with green and labeled with an "S") and destiny (colored with red and labeled with an "D") node have all the \(f_{2}\) associated costs distributed, which generates only two options to minimize each function.
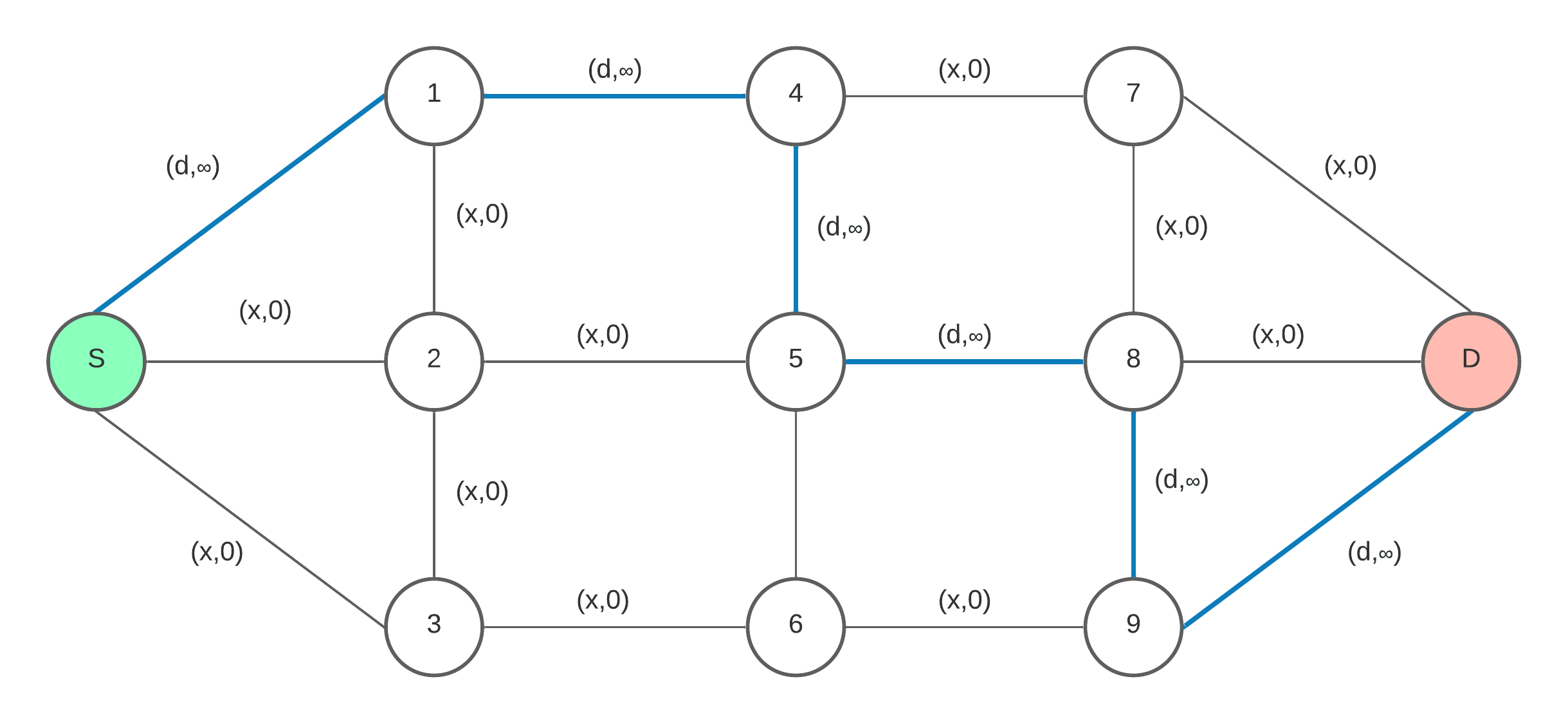
For the formal explaining of the problem nature, see the enunciated terminology described below:
Be
\(D: \text{Set of optimal links selected by Dijkstra's Algorithm}\)
\(C_{1}: \text{Set of optimal links to minimize} f_{1}\)
\(C_{2}: \text{Set of links where there are costs associated with} f_{2}\)
where from the pedestrian traffic displacement model, the following sets relationships occurs:
\(C_{1} \epsilon D\)
\(C_{2} \epsilon D\)
Single cost approach to solution heuristic
For the solution heuristic we proceeded to use Dijkstra algorithm with a unique cost calculated from the weighting of the normalization of the \(f_{1}\) and \(f_{2}\) costs. For this, the following scale characteristic normalization method was applied:
\[f_{1}^{'}(i, j) = \frac{f_{1}(i, j) -min(f_{1})}{max(f_{1}) -min(f_{1})}\]
\[f_{2}^{'}(i, j) = \frac{f_{2}(i, j) -min(f_{2})}{max(f_{2}) -min(f_{2})}\]
Where \(f_{k}^{'}(i, j)\) is the normalization of the scaling characteristic of \(f_{k}\) in the link of node \(i\) and node \(j\). \(max (f_{k})\) corresponds to the maximum value in the data set of the function \(k\). For the case of both functions, the maximum value was the integer \(99999\), since that was the default value in the cost matrix where there was no link between a pair of nodes. Finally, \(max (f_{k})\) is the minimum value in the data set of the function \(k\). For \(f_{1}\) it corresponded to the link between nodes of shorter length, and for \(f_{2}\) it was the minimum number of students who traveled on a link given a cycle, day and time.
Finally, the costs of the normalized functions were weighted through the weights that were later defined from the input parameters entered by the user, and they were assigned to a new function. Likewise, from the new function, we defined the heuristic solution that would have as parameters the inputs received by the front-end of the mobile application:
\[F(i,j) = w \cdot f_{1}^{'}(i, j) + (1-w) \cdot f_{2} ^ {'}(i, j)\]
\[H(s,d) = Dijkstra(F, s, d)\]
Where \(F\) is the function that stores the weight of the two initial normalized functions. \(w\) corresponds to the weight that the user implicitly enters as a parameter in the front-end to give a weight to each function. \(Dijkstra\) is the function that returns the optimal links given the unified cost function \(F\), a source node \(s\) and a destination node \(d\) given a cycle, day and time. Finally, \(H\) is the function that represents the problem’s heuristic solution. Once the heuristic solution was modeled, the results of the algorithm were compared with the solutions provided by the Pareto Front in different scenarios.
Results comparison and validation with the Pareto Front
For the validation of the results produced by the heuristic developed with the Pareto Front points, we defined different scenarios to vary the pedestrian traffic given a cycle, day and time with the same origin and destination node in each scenario. This was made with the objective of comparing how is the variation of the optimal route of two points from the assignment of different costs of \(f_{2}\) (since the costs of \(f_{1}\), being the length of each link between nodes remained fixed in the different executions. However, it should be noted that the accumulated cost of \(f_{1}\) changes from the different routes selected).
| Scenario Number | Academic Cycle | Day | Schedule | Source Building | Destiny Building | |
|---|---|---|---|---|---|---|
| 1 | 1 | Wednesday | 10:50 - 11:00 | J. M. Santodomingo | Mario Laserna | |
| 2 | 1 | Monday | 13:30 - 14:00 | J. M. Santodomingo | Mario Laserna | |
| 3 | 1 | Thursday | 13:30 - 14:00 | J. M. Santodomingo | Mario Laserna |
As it is observed in Table 4, the scenario specifications include the chosen Academic Cycle (semester period), day, schedule (interval of time where student pedestrian displace through the university campus) source and destiny building. As it observed, the source and destiny building remain fixed through all the three scenarios, where the days and schedule are variable. This is done with the purpose of having the same source and destiny for all scenarios, varying the time parameters that change pedestrian traffic peaks and volumes.
For the generation of the Pareto Front, the method described in Section 4.3 was used. Regarding the values of \(w\) for \(F\), different values were iterated in the domain of \(w\) (\([0, ..., 1]\)) to observe the obtained points by the heuristic in each iteration.
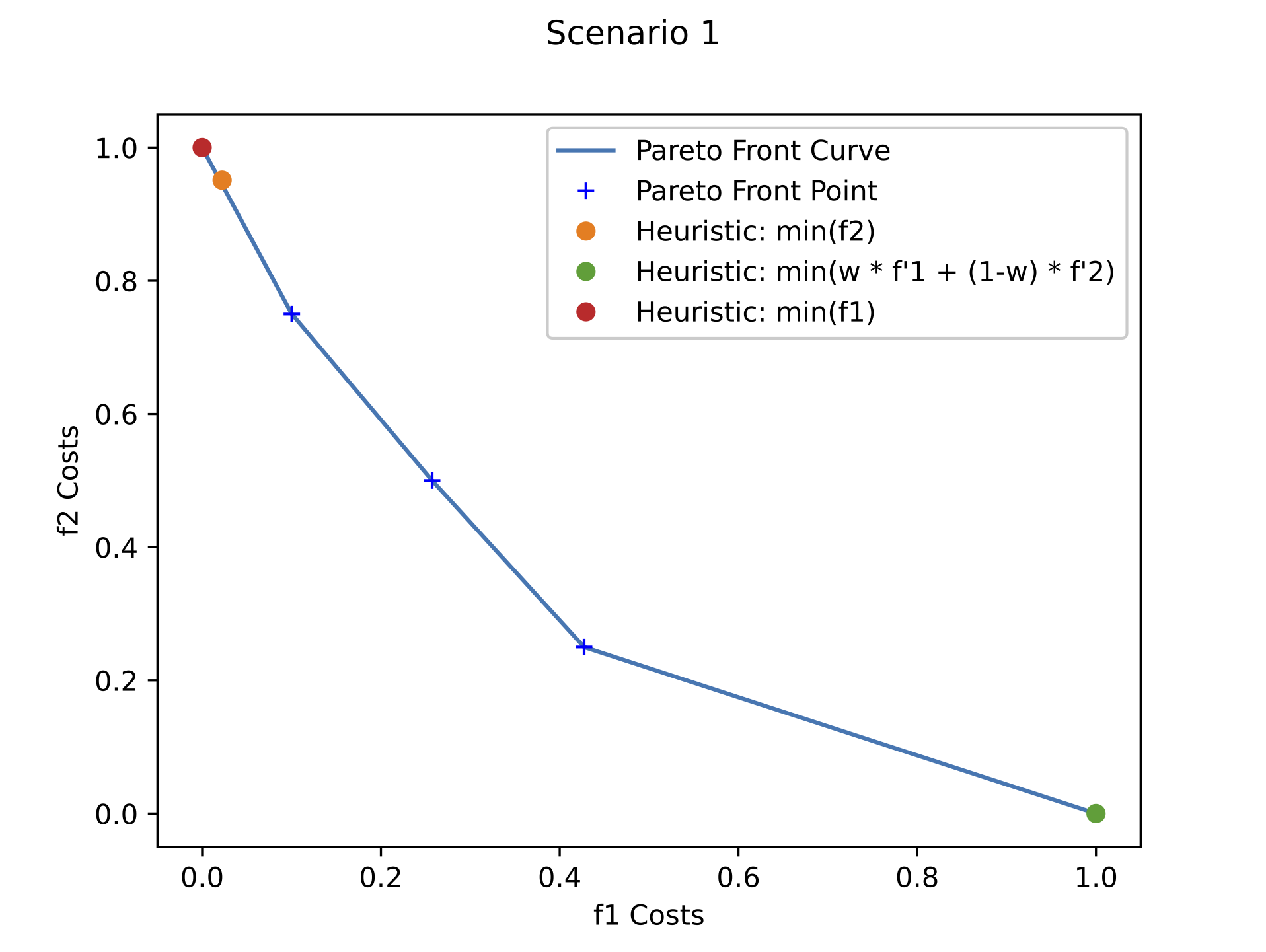
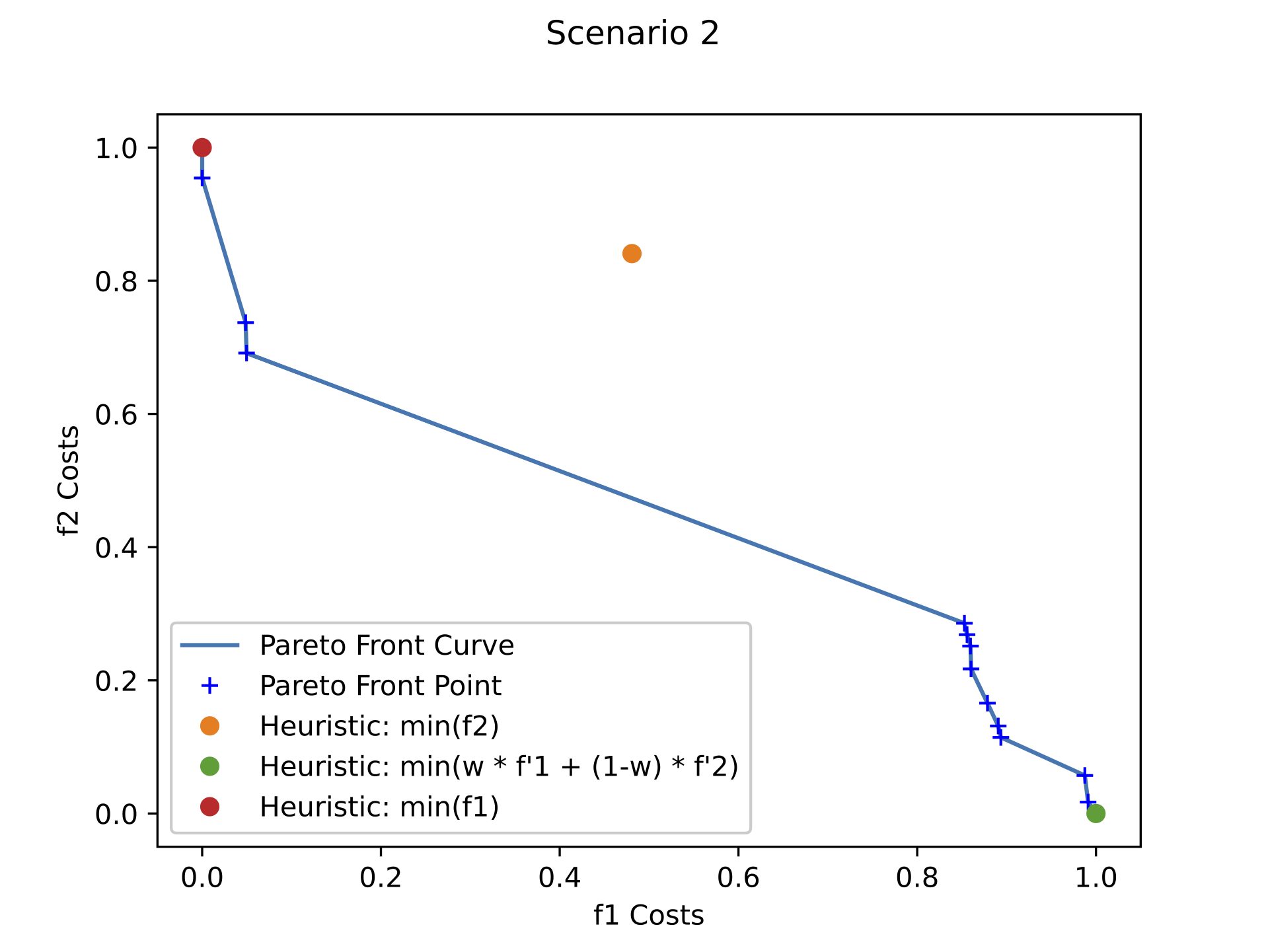
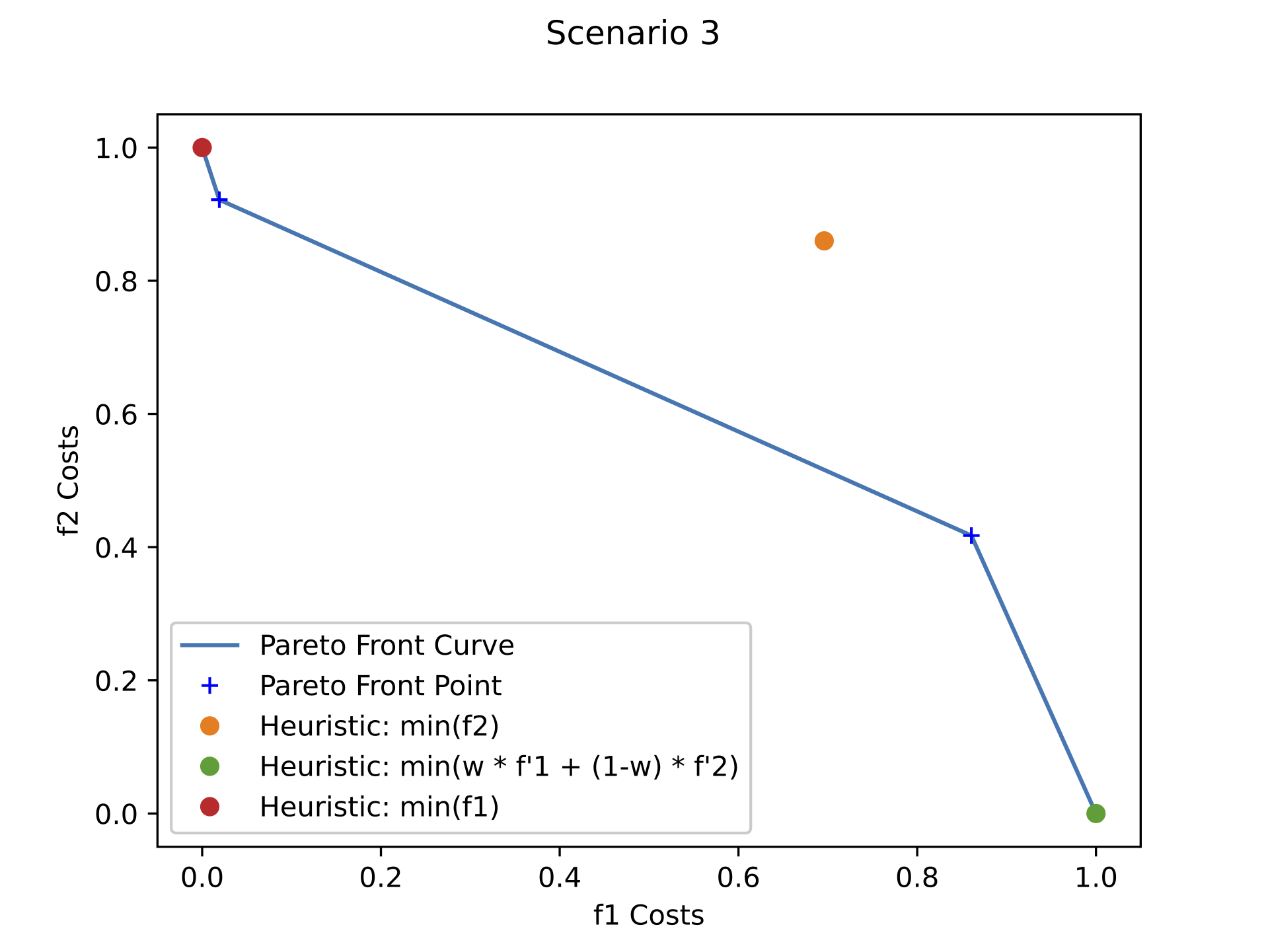
It is observed in Figure 4 that different points were got from the Pareto front, as well as the heuristic solution from the same source and destiny buildings, but with different student pedestrian traffic and assigned weights for each \(w \epsilon F\). For the Pareto Front and Heuristic solutions obtained for Scenario 1 (subfigure a), it is observed that given the pedestrian traffic for the 10:50-11:00 schedule on Wednesday, it was possible to obtain more intermediate solutions given the concavity of the curve compared to the other scenario fronts. For Scenario 2 and Scenario 3 (subfigures b and c respectively), the optimal solutions given by the mathematical model were more approximate to the optimal solution that only solve for either \(f_{1}\) or \(f_{2}\) functions. Also, for this two scenarios, it was found that the solution given by the heuristic when minimizing only \(f_{2}\) was not included in any of the Pareto Front resulted in the executed mathematical model solving.
As main evidence, we observed that since it is a problem with only two optimal solutions available the Pareto Front, points were generated particularly at the limits of each function. Likewise, it was obtained that when \(w \neq 0\) or \(w \neq 1\), the heuristic yielded the same solution in each iteration. Therefore, the solutions thrown by the heuristics behave as if they were only minimize \(f_{2}\), this is due to a single cost function where the costs of \(f_{2}\) associated with the optimal \(f_{1}\) paths made the heuristic look for paths that were not optimal for \(f_{1}\) in order to minimize weight associated with \(f_{2}\). For such reason it can be seen that the algorithm solution does not generate optimal results to minimize \(f_{1}\).
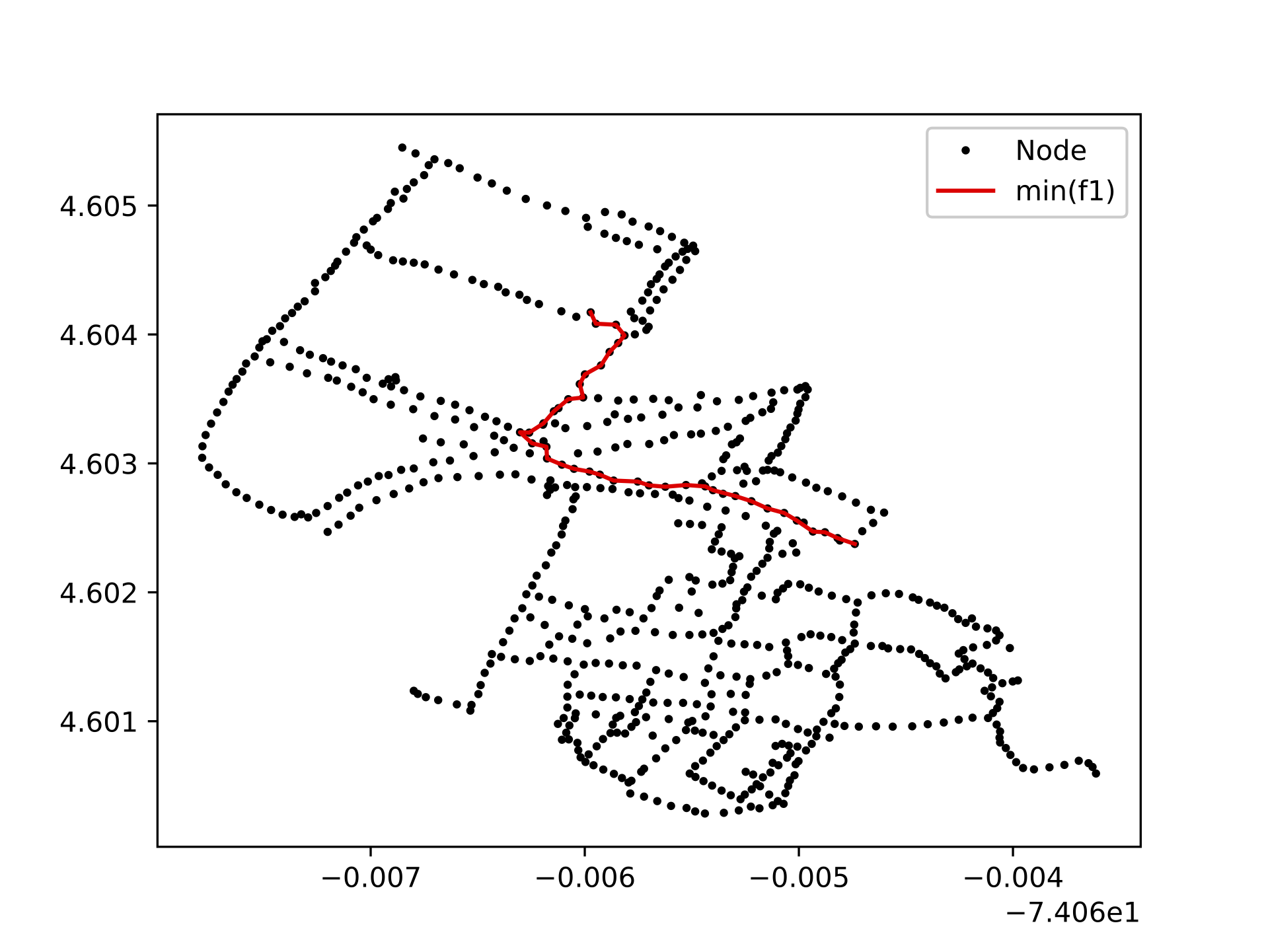
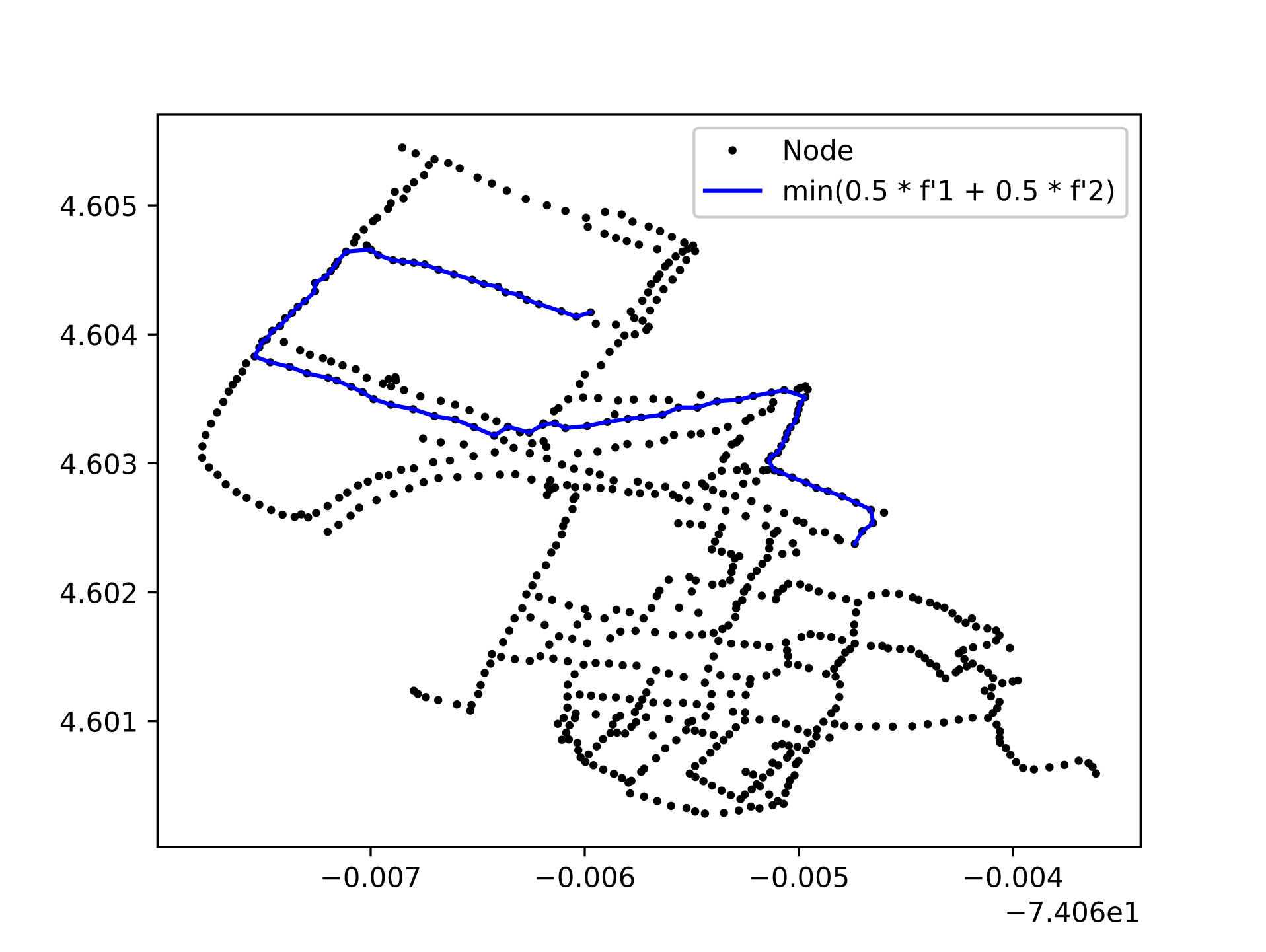
Thus, in the iteration when \(w = 1\)- which is when the heuristics were only considered minimizing \(f_{1}\)- a solution was got at one end of the Pareto Front, where the associated cost of \(f_{1}\) is minimized and the cost associated with \(f_{2}\) is maximized. However, on iteration when \(w = 0\), which is the case where the heuristic only minimized \(f_{2}\). We found that although that the solutions obtained minimize the accumulated cost of \(f_{2}\) with respect to the iteration scenario when \(w = 1\), These solutions are solutions dominated by the points that make up the Front, and additionally, it is a non-optimal solution when minimizing \(f_{2}\) compared to the solutions obtained in the iterations when \(w \notin \{0,1\}\) For additional information of the described scenarios, see Figure 5, in where the optimal path selected by the heuristic is shown for the different values iterated by \(w\) in its domain. Note the similarity of routes chosen when the heuristic only minimizes \(f_{1}\) or \(f_{2}\) (subfigure a and c respectively) , and as in a different scenario (subfigure b ) increases the cumulative cost of \(f_{1}\) to minimize the cumulative cost of \(f_{2}\). From the observations derived from the results, and from the naturalness of the modeled problem described in Section 4.2, we decided to only expose two possibilities of paths in the mobile application, where each option corresponds to the minimization of each function. Therefore, to obtain these results, the domain of \(w\) was configured to only take the values of \(1\) and \(0.5\) (which is a decimal that assigns equal weight to both normalized functions).
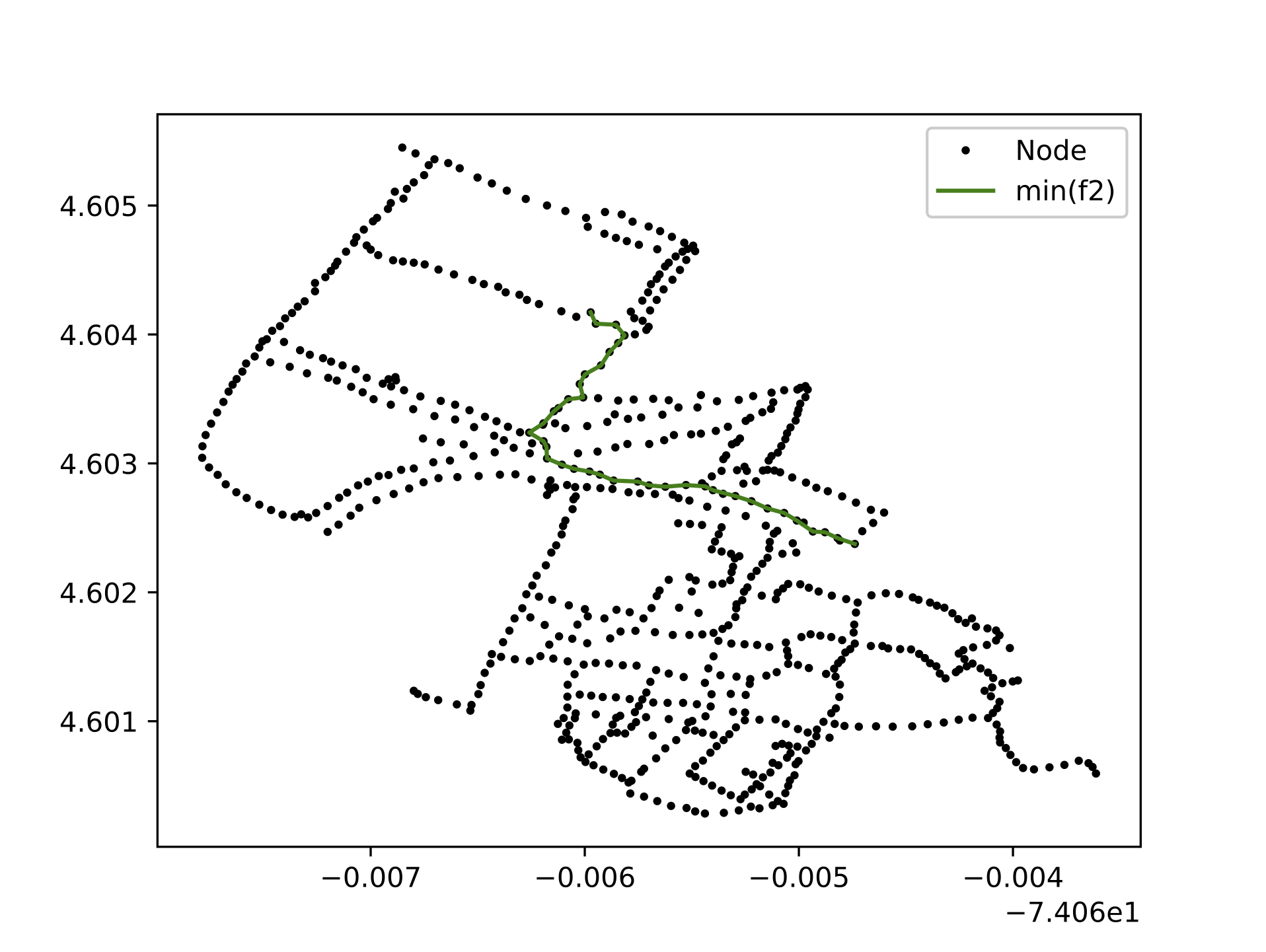
Results comparisons and validation based on the Mathematical Model
From the configurations established for the solution heuristic in the Section 4.2 - where \(f_{1}\) and \(f_{2}\) were equally normalized and weighted to minimize \(f_{2}\) - The execution times used by both the mathematical model and the heuristics to minimize \(f_{1}\) and \(f_{2}\) were compared, as well as the values established by the functions in each scenario.
The mathematical model was configured in the optimization framework Pyomo [15] and the heuristic was written and executed in a script written in the programming language Python. The specifications of the chosen and executed scenarios were set up as the same scenarios for the Pareto Front validation (which details can be observed in Table 4).
First, the execution times of each scenario were compared, where it was noted that the execution times got by the heuristic are approximately \(98.45 \%\) less than the times obtained by the mathematical model. The previous result facilitates the response time of the calculation of an optimal route when the heuristic is integrated as a service to the mobile application.
Both the heuristic and the mathematical model were executed on an Intel Core i5-6200U, 2.3 GHz, 7.7 GiB. Additionally, in the executions made by Pyomo the mathematical model was solved using the GLPK solver. The execution times details and values for each scenario can be observed in the Table 5, Table 6 and Table 7. Subsequently, the resulting values of \(f_{1}\) and \(f_{2}\) were compared for each tool of the minimization of each function of each scenario. As it is observed in Table 6 and Table 7, the heuristics got relatively lower values for \(f_{2}\) compared to the mathematical model in each case of minimization of \(f_{1}\) (It should be noted that in these cases the two tools got the same result for \(f_{1}\)), while in the cases of minimization of \(f_{2}\) each tool had the same results for this function.
| Scenario Number | Function to minimize | Heuristic Execution Time (sec) | Mathematical Model Execution Time (sec) |
|---|---|---|---|
| 1 | \(f_{1}\) | 2.761 | 182.504 |
| \(f_{2}\) | 2.519 | 164.167 | |
| 2 | \(f_{1}\) | 2.522 | 153.907 |
| \(f_{2}\) | 2.423 | 171.088 | |
| 3 | \(f_{1}\) | 2.544 | 161.058 |
| \(f_{2}\) | 2.695 | 165.645 |
| Scenario Number | Function to minimize | Heuristic value for \(f_{1}\) (units) | Mathematical Model for \(f_{1}\)units |
|---|---|---|---|
| 1 | \(f_{1}\) | 3.08 \(\cdot 10^{-3}\) | 3.08 \(\cdot 10^{-3}\) |
| \(f_{2}\) | 6.58 \(\cdot 10^{-3}\) | 6.99 \(\cdot 10^{-3}\) | |
| 2 | \(f_{1}\) | 3.08 \(\cdot 10^{-3}\) | 3.08 \(\cdot 10^{-3}\) |
| \(f_{2}\) | 6.68 \(\cdot 10^{-3}\) | 7.48 \(\cdot 10^{-3}\) | |
| 3 | \(f_{1}\) | 3.08 \(\cdot 10^{-3}\) | 3.08 \(\cdot 10^{-3}\) |
| \(f_{2}\) | 6.64 \(\cdot 10^{-3}\) | 7.11 \(\cdot 10^{-3}\) |
| Scenario Number | Function to minimize | Heuristic value for \(f_{1}\) (units) | Mathematical Model for \(f_{1}\)units |
|---|---|---|---|
| 1 | \(f_{1}\) | 495 | 495 |
| \(f_{2}\) | 5 | 5 | |
| 2 | \(f_{1}\) | 540 | 540 |
| \(f_{2}\) | 19 | 19 | |
| 3 | \(f_{1}\) | 682 | 682 |
| \(f_{2}\) | 35 | 35 |
Mobile Application Design
We implemented a REST API software architecture style [16] using the web framework Flask [17] written with Python scripts. Likewise, the steps and instructions for the heuristic solution (see Section 5.2) were developed in the programming language Python. The input parameters that the REST API received for the solution heuristic to compute the optimal path were: a string text containing the initials of the building in which the student is located (s); a string text containing the acronym of the building the student wants to go to (d); a string text that shows the academic cycle in which it is desired to calculate pedestrian traffic. By default, this value corresponds to "1" (cycle); a string text that indicates the day set to calculate pedestrian traffic (day); a string text that indicates the schedule for changing classes of pedestrian traffic. Note that class change hours are expressed in the 24-hour system (schedule); an integer that shows which function it is wanted minimize (1) or if it is wanted to minimize the transport cost function (0), if it is wanted to minimize the interaction cost function (w). For more details on what these functions represent, see Section 4.
It should be noted that these methods are received by the server through a POST request. To test the connection between the Flask server and the client, the server was run on a local machine Intel Core i5-6200U, 2.3 GHz, 7.7 GiB machine. and perform client API requests through the Postman [18] software.
For the mobile application development, we designed it in a way that it could be executed in the operating system Android 9 [19]. Likewise, through the programming language Kotlin [20] and the graphical interfaces for the design of the UI components provided by the Android Studio development environment, we implemented the front end logic and graphical components to show the probability of susceptibility and the accumulated distance when traveling a route.
For the generation of the university campus map, a Google Maps software development kit was used available for Android [21]. In Figure 6, it can be observed the graphical interface of the application with the susceptibility probability and the accumulated distance in the lower bar as well as the optimal route drawn. It should be noted that the icons and figures of the application were taken from the web page https://www.flaticon.com/ [22].
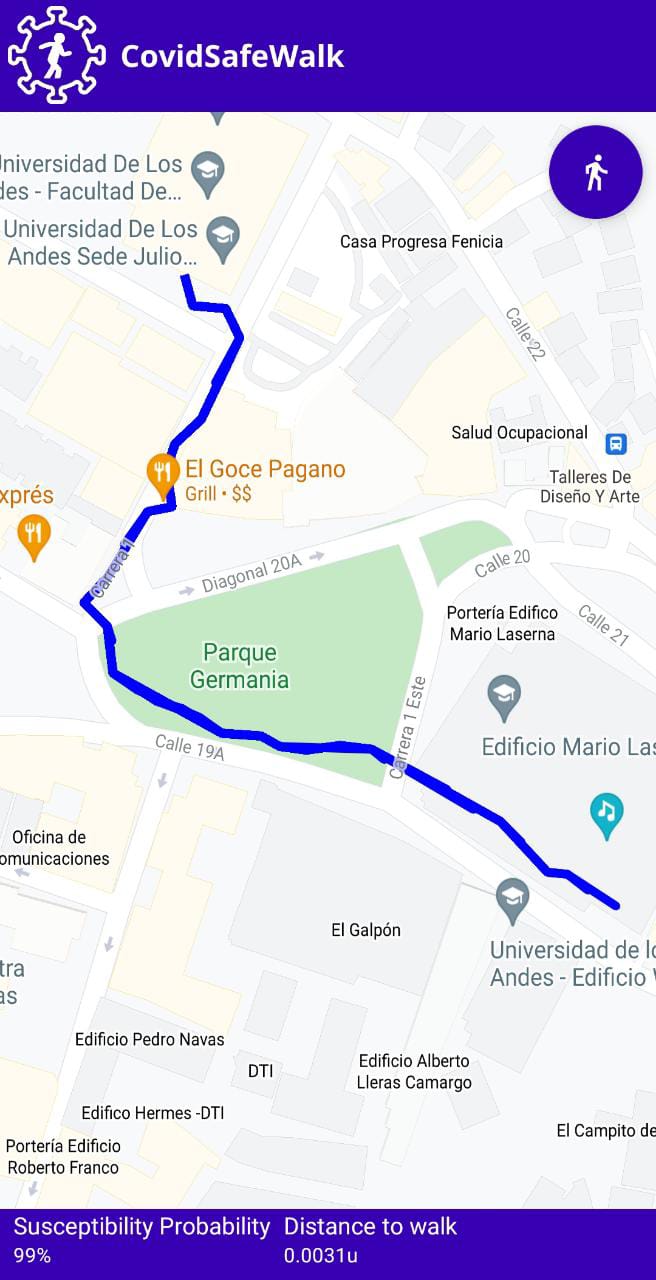
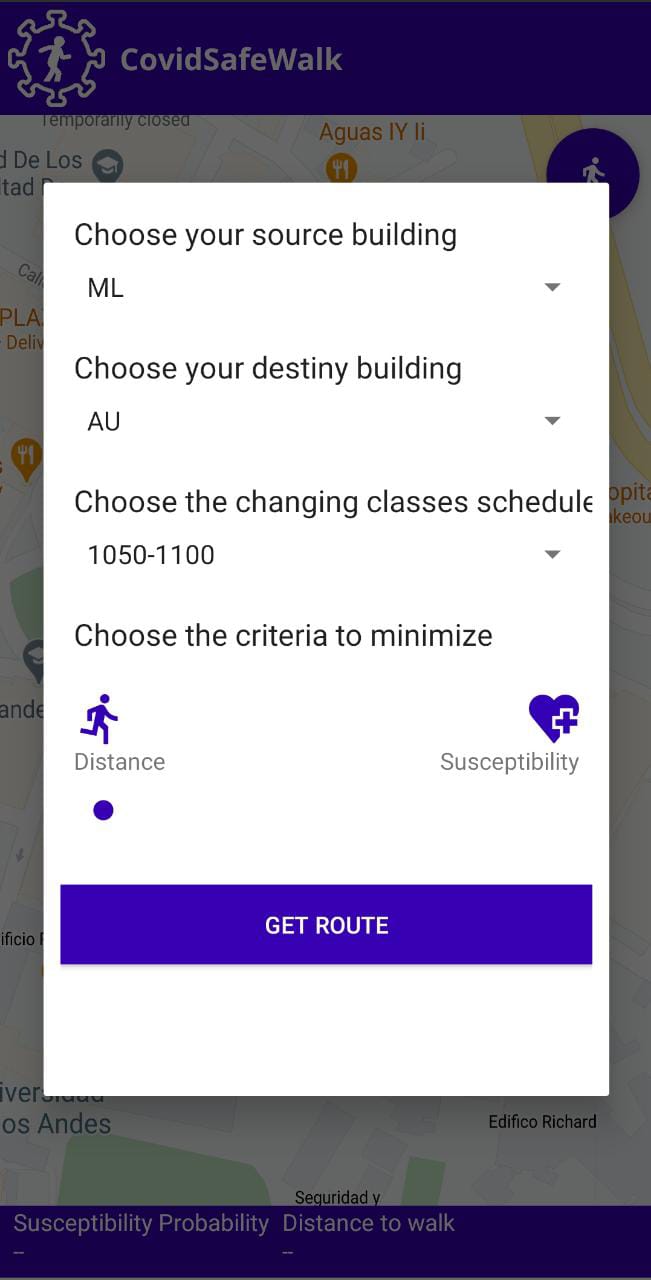
For the selection of parameters to be sent to the server, a graphical Android component (AlertDialog) was used to create a form that would allow a student to select the source building, the destiny building, the opening hours, change of classes available for that day and the route criteria to be minimized. To get significant records of the students’ trajectory for the generation of pedestrian traffic, we assumed that the default academic cycle parameter was \(1\). Likewise, the day was automatically assigned according to the current day on which the application was used. If the student uses the application on Sunday - the day on which the university does not hold academic classes - the application assigns Monday as the default parameter. In Figure 6, it can be observed the parameter selection form.
Once the parameters were selected, when pressing the Get Path button of the form, the application - using the HTTP Android Volley [23] library - send the request POST to the IP address of the local machine where the server was deployed. Once the server response is received, the application updated its interface, showing in the lower bar the susceptibility probability that the user has when traveling the route, as well as the accumulated distance that they have to walk. An example of how the route is drawn in the application can be observed in the Figure 6.
Software Architecture
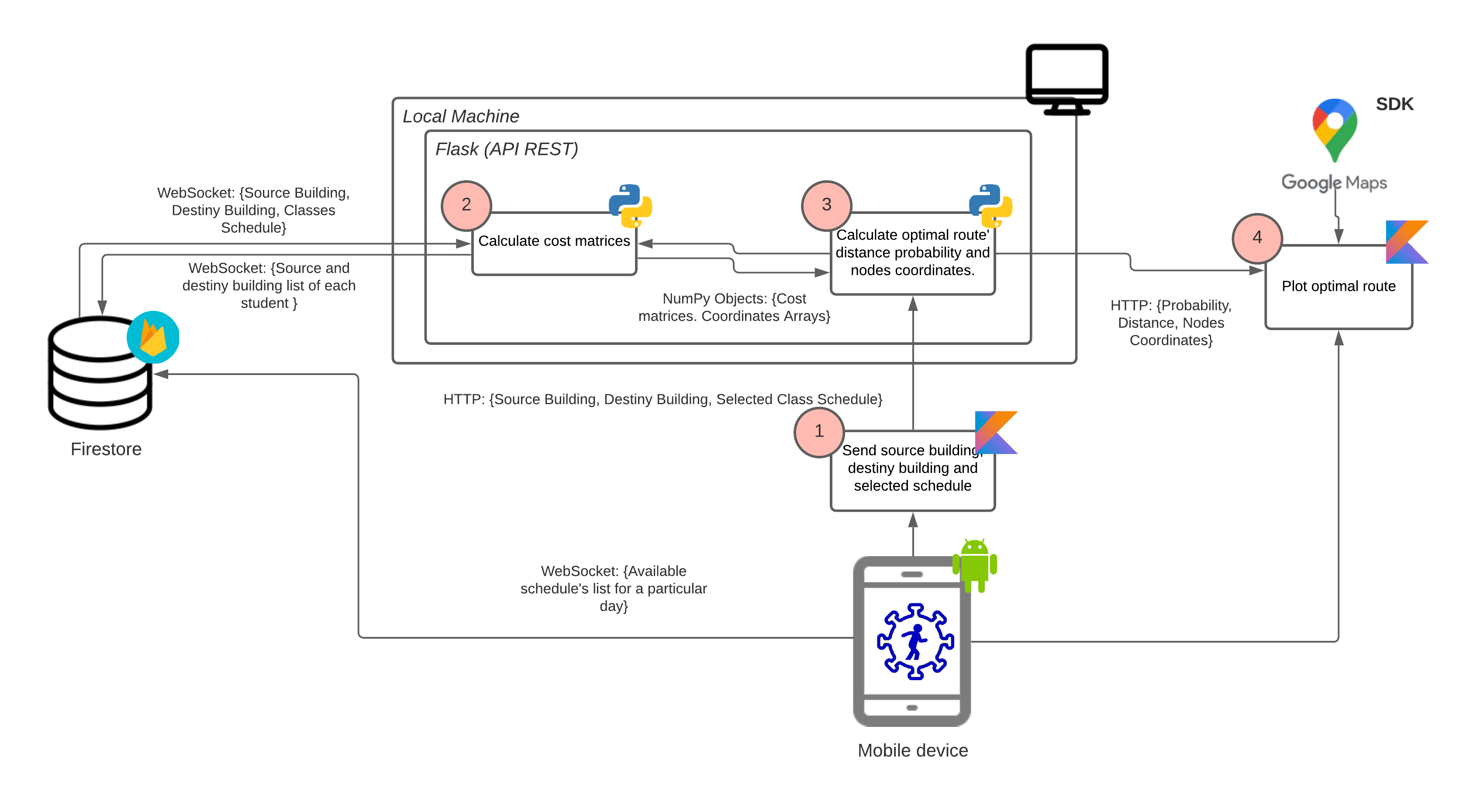
In summary, once the back end and the front end of the application solution to the initial problem were established, a software architecture was built where the following sequence of steps is performed in order to obtain a route that minimizes one of the two criteria to consider in the problem Following is a summary of the general process that the mobile application follows in order to calculate an optimal path:
The user through the mobile application selects the parameters to calculate the most optimal route, among these parameters is the selection of the function to minimize.
The server receives these parameters and proceeds to calculate the transport cost matrix in order to generate pedestrian traffic given the time parameters assigned by the user, and likewise, assigns these costs to the interaction cost matrix for each link of the university graph. The records of the routes of all students are obtained from the platform Firebase [11]
Once the cost matrices are obtained given the scenario assigned by the user, the solution heuristic is executed for the chosen function and the susceptibility probability, the accumulated distance and the list of coordinates of the nodes of the optimal route.
Once the mobile application receives the values from the server, it proceeds to graph those values and path in the graphical interface.
In Figure 7 it is observed the final architecture diagram. As it is displayed, in the upper right corner of each activity / device it can be observed the programming language, software or platform used. In the upper left corner is the step number of the sequence of steps followed by the process execution. The intermediate texts between the arrows connecting each activity / device show the communication protocols used.
Validations
To observe the final product functionalities through its graphical interface, the scenarios presented in Table 8 were considered and validated to notice the variation between the probability of susceptibility and the accumulated distance when minimizing each criteria, given the different origin-destination buildings and pedestrian traffic on a certain day and class change schedule. These results describe the obtained values on the mobile application UI for each criteria based on the selected criteria to minimize. For the Susceptibility Probability column, it is shown when choosing the Susceptibility criteria in the mobile application the probability is reduced compared to the same scenario when the Distance criteria is selected for the path calculation. As it is observed, the variables Susceptibility Probability and Distance are inversely proportional It should be noted that the scenarios presented took Thursday and "1" as the default day and academic cycle respectively, since the tests were made on that specific day of the week.
| No | Schedule | Source Building | Destiny Building | Selected Criteria | S. Probability value (percentage) | A. Distance value (units) |
|---|---|---|---|---|---|---|
| 1 | 10:50 - 11:00 | Mario Laserna | Aulas | Distance | 99% | 0.0016 |
| Susceptibility | 85% | 0.0025 | ||||
| 2 | 13:30 - 14:00 | Mario Laserna | City U | Distance | 99% | 0.0023 |
| Susceptibility | 66% | 0.0037 | ||||
| 3 | 10:50 - 11:00 | J. M. Santodomingo | Mario Laserna | Distance | 100% | 0.0031 |
| Susceptibility | 99% | 0.0068 |
Conclusions
Based on this research, a mathematical model and solution algorithm were developed in order to optimize the most important criteria to be considered by a Universidad de Los Andes student: displacement effectiveness and COVID-19 contagion risk. Therefore, the mobile application that was developed allows a student pedestrian to access in a easy and quickly way a software tool that optimizes the COVID-19 risk contagion problem from a mobility pattern and displacements perspective. Likewise, based on the pedestrian traffic simulation and the modeled cost functions, we could generate and understand a pedestrian agglomerations’ approximation based on a set of student classes that had time attributes. Moreover, based on the data hierarchy and aggregated pedestrian mobile users data, and considering the case the developed mobile application is used by multiple users, strategies can be established for data analysis from the different hierarchy data levels (day, academic cycle, etc.). This activity has the purpose to understand the mobility patterns that university students modelate, and therefore, enables high-level decision making processes that avoid pedestrian agglomerations at a specific time.
Performance and limitations
Through the research development we found perfomance cases in which from the variables quantity and the initial costs functions modeling cause additional response times in the solution software execution. Following are described the events that had an impact on the final product performance, with considerations to optimize and improve those respective events.
University campus graph modeling optimization
Given that the mathematical model costs matrices were \(n x n\) size, where \(n\) was the number of consecutive nodes established for each existing path on the university campus, and given the node network size of the university campus (which were \(700\) approx.) execution times for Pareto Front and mathematical model solving execution were longer than 1 minute. Therefore, we consider to reduce the university campus nodes quantity, suppressing innecesary intermediary nodes between the beginning and end of each existing path on the university. With this feature, execution times of algorithms and mathematical models solving that consume the matrices costs would be reduced.
Student pedestrian traffic accuracy and bi-objective problem handling
As it was described in Section 5.1, student pedestrian traffic model was only established from the university’s optimal route set. However, given that a city displacement patterns depends of external factors, like an specific day, date, near events and diverse social conditions, we consider to model a mobility patterns characterization of the Universidad de Los Andes community, given the multiple circumstances and situations that can affect the displacement patters. Also, this research only considered undergraduate students as the only pedestrians that travel the university network, which only considers one group as the university pedestrian traffic. Hence, we consider to include displacement patterns that are made from the multiple pedestrian university groups - as teachers, staff, etc. - as this groups could have a bigger significance on the pedestrian traffic modeling on the university campus. Nevertheless, the research objective was to guarantee a student safety based on a COVID-19 risk contagion as well a travel displacement optimization in a post-pandemic scenario. Therefore, and given the fact that there is no sufficient data to model pedestrian traffic on a pandemic scenario as the date of publishing this work, it is suggested to have in consideration current variables that impact on the pedestrian traffic modeling (like social distancing) with the aim of modeling a displacement pattern as accurate as possible for this new scenarios.
Susceptibility probability function accuracy
During the development of the mathematical model and the function that represents the interaction cost (\(f_{2}\)), it was noted that the function and the modeling of the susceptibility probability of contracting COVID-19 was completely dependent on [5]. As for the readers awareness, it should be noted that the previous reference contains preliminary and ongoing research as the probability function is still being function as the publishing date of this work. It should be noted that, as the date of developing this project, there was lack of studies and modeling data that we could based on for modeling an accurate COVID-19 risk contagion probability. Therefore, it should be noted that the function calibatrion parameters should be interpreted as placeholder values and the susceptibility probability function relies primary on the encounters students have during their displacements. We consider the importance to validate and implemented accurate and certified probability COVID-19 risk contagions functions that rely more on approved researched and have an advance in the development of this topic.
Future works
Susceptibility probability function parameters calibration based on published future works
Given the precariousness and early research of the studies published by [5] to define the susceptibility probability of COVID-19 as of the date of releasing this paper, it is expected to seek for researches with more exact parameters for the probability function. In future, studies of epidemiological models about the coronavirus may offer more specific functions that model the contagion probability or susceptibility of the virus, which is relevant for the calibration of the interaction costs of the initial problem.
Medical domain approbal for the proposed solution
We considered that a validation process must be complemented from the medical domain point of view in the future. In other words, the inclusion and approval of health entities that comprehend the COVID-19 contagion processes could help to calibrate and adjust our research to propose a joint solution validated from the computational and medical point of view.
Multi-user model and design
This iteration of the project only considered a mono-user scenario interacting with the mobile application. However, the release of a mobile application where multiple users make use of it opens the scenario for including the users application within the calculated pedestrian traffic models. In this case, it is suggested that in addition to including additional pedestrian traffic data in the back end of the mobile application, the optimal routes taken by other users of the mobile application should be included. This allows the incorporation of a pedestrian traffic model that takes into account the multi-user use of the mobile application.
Software architecture impromevement
Given that the server deployment back end is located on a local machine and network, and based on the consideration of a multi-user scenario of the mobile application, we suggested that the server should be deployed and configured on a cloud computing service platform . It should be considered to establish better response times between server and client, or create communication protocols that do not degrade the user experience when requesting an optimal route or the calculations made by the backend service.
Authors’ Information
Juan E. Cantor obtained a degree in Computer and Systems Engineer (2020) at the Universidad de Los Andes in Bogota, Colombia. He currently works as Java technical lead at Scotiabank Colpatria bank. His research interests are mathematical optimization, mobile application development, and software architecture.
Germán A. Montoya obtained a degree in Electronics Engineering (2006) at the Universidad Pontificia Bolivariana in Medellín, Colombia. He also obtained a Ph.D. in Engineering (2017) at the Universidad de Los Andes in Bogota, Colombia. Currently, he is a Postdoctoral Assistant at the Universidad de Los Andes in the System and Computing Engineering Department. His main interests are mathematical optimization, simulation, and wireless sensor networks.
Carlos Lozano-Garzon received a degree in System Engineering (2002) at the Universidad Nacional de Colombia in Bogota, Colombia. He also received a Ph.D. degree at both Universidad de Los Andes, Colombia, and Universitat de Girona, Spain in 2017. He is currently Assistant Professor at the Universidad de Los Andes, Colombia in the System and Computing Engineering Department. He worked as a professor at the Universidad Nacional de Colombia, among others, as well as a visiting professor at the Universidad Nacional de Asunción, Paraguay. His research interests are Network Optimization from a multi-criteria perspective, Smart Mobility: Vehicle Networks and Intelligent Transport Systems, Internet of Things, and Network Security.
Authors’ Contributions
Juan E. Cantor participated in the conceptualization and methodology as well as the original draft preparation, the mathematical optimization model, the software tests, validations, and final review of the manuscript.
Germán A. Montoya participated in the conceptualization and methodology as well as the methods review and final review of the manuscript.
Carlos Lozano-Garzon participated in the conceptualization and methodology as well as the methods review.
Competing Interests
The authors declare that they have no competing interests.
Funding
No funding was received for this project.
