Introduction
The idea of weather prediction using analog ensembles is not new. It was described as early as 1969, by Lorenz [1] who concluded that such a method would not work. However further works managed to prove the usefulness of this approach in a much more limited scope, in fields ranging from meteorology to flood study, especially thanks to the decisive contributions of Van Den Dool [2], [3].
The Analog Ensemble (AnEn) method enables to improve the accuracy of a deterministic numerical weather prediction (NWP) model that makes a forecast. Alongside this forecast, historical forecasts are also available (a record of forecasts from NWP at past dates), as well as historical observations (a record of real meteorological data observed in a given place). Then, to improve forecasting accuracy, the forecast is compared to historical forecasts. The historical forecasts analogs to the current one are kept, and the observations corresponding to the dates of the best analogs are used to improve the forecast value. The name of the method comes from there: past forecasts close to the current one are called analogs, and these are used to obtain an ensemble of past observations.
The AnEn method is mostly used as a post-processing procedure. A deterministic NWP forecast model reports on a possible state of the atmosphere among many possible states. As the predicted state does not always match reality (due to the limitations of the model and its inputs), it is useful to have a probability distribution function (PDF) of the possible states that quantifies the uncertainty associated with the prediction. The forecast PDF can be estimated using a set of \(n\) past validation observations corresponding to the \(n\) best analogs (past model forecasts) to the current NWP model forecast [4]. As the AnEn method allows us to quantify the uncertainty associated with the forecast of a meteorological variable, this method was also used to generate probabilistic wind power forecasts [5].
In the field of meteorology, a significant contribution to the use of the Analog Ensemble method was made by Monache et al., [6] having been refined [4] and applied to a variety of operational scenarios [5], [7], [8], where its accuracy and usefulness were clearly demonstrated.
Since the AnEn method provides a prediction based on past observations, it results in an efficient downscaling procedure that eliminates representativeness issues. These arise from the fact that observations and model output can be associated with quantities averaged over different spatiotemporal scales [6].
This article is an extended version of previous work [9]. It focuses on the problem of making weather predictions for a given location where no forecast is available, using meteorological datasets from nearby stations. With this aim, the AnEn method was applied to a hindcasting problem, where the time-series of a meteorological variable in a given location was reconstructed using data from neighbor weather stations. To discover ways to improve on the original AnEn method, alternative metrics to determine the analogs were considered, and their performance was compared, allowing us to find out which ones exhibit the best accuracy. To investigate the impact of more than one predictor station on the performance of the hincasting, this evaluation was conducted both with a single predictor station dataset, and also using the datasets from two stations.
The rest of this paper is structured as follows. Section 2 presents the AnEn methodology, the mathematical formulation of all the metrics and prediction methods considered, and the definitions for error quantification. Section 3 describes the field data used in this study, the numerical results produced by the computational execution of the AnEN methodology and an analysis of those results. Section 4 concludes with final remarks and lays out directions for future work.
The Analog Ensembls Methodology
The Analog Ensemble method is relatively simple. Having an accurate similarity metric is crucial, though, for the success of the forecasting. This section presents alternative metrics and prediction methods that can be used for this purpose. It also describes the tools used to evaluate the performance of the different metrics.
Applying the Analog Ensemble Approach
The classical AnEn method builds on an observed dataset consisting of real records of meteorological variables, and on a historical dataset that corresponds to a time-series from a Numerical Weather Prediction (NWP) model used to forecast [4], [5] or hindcast [10] meteorological data.
Figure 1 illustrates how the Analog Ensemble (AnEn) method is used in this work, to predict the values of a weather station using another station. Comparing this scenario with the classical application of the AnEn method, the dataset from the predictor station corresponds to the historical dataset, and the dataset from the station to be predicted corresponds to the observation data set; moreover, real measurements from meteorological stations were used as the historical dataset.
Historical and observation datasets must exist over a Training Period. The larger this period, the better the AnEn method performs [11]. The other period considered is the Prediction Period (or Reconstruction Period in an hindcasting context), in which only data from the predictor station is available.
As depicted in Figure 1, the AnEn procedure is implemented in three steps for each time step to predict or reconstruct. Firstly, in step the values analog to the prediction are obtained by scanning the historical dataset from the predictor station. Analogs are past occurrences deemed close enough to the current prediction, classified as such according to an analog metric. Step consists of matching these analogs with the corresponding observations at the target station. Step consists of estimating the target value with the past values matched to the analogs (e.g., weighted average).
Metrics Used to Find Analogs
In the present work various metrics were used to assess and compute the similarity between meteorological data of the predictor station. By analogy with the original AnEn method, the data from the predictor station included in the prediction period will be referred to as forecasts.
The first metric used was the one originally established by Monache [4] for the AnEn method. It will be simply referred to as the Monache metric from now on. This metric is based on the Euclidean distance: it computes the difference between the values of atmospheric variables in two windows of time. One of the windows is the forecast and the other belongs to the preceding historical dataset.
The Monache metric is given by Equation [1] and the meaning of its terms is shown in Table 1.
\[ \sum_{i=1}^{N_v} \frac{w_i}{\sigma_{fi}} \sqrt{\sum_{j=-k}^k(F_{i,t+j}-A_{i,t'+j})^2} \label{monache0}\]
| \(F_t\) | Forecast at given time \(t\) in the prediction period. |
| \(A_{t'}\) | Analog forecast at a time \(t'\) in the training period. |
| \(N_v\) | Number of meteorological variables taken into account when comparing forecasts. |
| \(w_i\) | Weight given to variable \(i\). |
| \(\sigma_{fi}\) | Standard deviation of variable \(i\) in the historical dataset. |
| \(k\) | Integer equal to half the width of the time window over which the metric is computed. |
| \(F_{i,t+j}\) | Value of the forecast at time \(t+j\) in the time window for a given variable \(i\). |
| \(A_{i,t'+j}\) | Value of the analog at time \(t'+j\) in the time window for a given variable \(i\). |
Considering \(F_{i,t}\) and \(A_{i,t'}\) as two vectors of size \(2k+1\), Equation [1] may be rewritten simply as presented in Equation [2]. \[ m_1=\sum_{i=1}^{N_v} \frac{w_i}{\sigma_{fi}} ||F_{i,t} - A_{i,t'}||, \label{monache}\] where \(||.||\) represents the Euclidean norm.
An alternative metric is obtained by normalising \(F_{i,t}\) as well as \(A_{i,t'}\) in Equation [2], resulting in Equation [3]. \[ m_2=\sum_{i=1}^{N_v} \frac{w_i}{\sigma_{fi}} \left\| \frac{F_{i,t}}{||F_{i,t}||} - \frac{A_{i,t'}}{||A_{i,t'}||}\right\|. \label{normalization}\]
Normalized vectors all have a norm of 1. The idea behind this reasoning is to look at the global weather pattern present in both forecasts. It can be seen that the basic Monache metric looks not only for a similar weather pattern, but also for similar numerical values to the various variables used in the forecast. As a consequence, it will not keep as an analog a forecast behaving exactly like the forecast to improve, but at higher or lower values. Normalization aims at solving this perceived problem. This method is called Normalized Monache, hereinafter abbreviated to Normalized.
Another approach is to consider the cosine of the angle \(\theta\) between vectors \(F_{i,t}\) and \(A_{i,t'}\), given Equation [4].
\[ \mathrm{cos}(\theta) = \frac{A_{i,t'}^T F_{i,t}}{\left\|A_{i,t'}\right\| \left\|F_{i,t}\right\|} \label{cos}\]
where \(A_{i,t'}^T\) denotes the transpose of vector \(A_{i,t'}\). The cosine can then be used to estimate the analog by means of the correlations between the two vectors, as demonstrated by K. Adachi [12] as presented in Equation [5].
\[ m_3=\sum_{i=1}^{N_v} \frac{w_i}{\sigma_{fi}} \mbox{ } \mathrm{cos}(\theta). \label{cosine}\] It is known that this metric behaves like the correlation coefficient, taking values between -1 and 1 (1 = maximum similarity). The idea of the cosine metric is thus to replace the Monache metric with the cosine of the angle between the forecast and the analog, keeping the analogs with cosine closest to 1.
Lastly, clustering can also be applied to this problem. Clustering is the partitioning of data into clusters of similar data. In this case each \(2k+1\) vector \(A_{i,t'}\) is assigned to a similar cluster. Each cluster constitutes an analog ensemble. Clustering the historical dataset produces several analog ensembles that can then be used immediately. The only task left is to assign the current forecasting to the good analog ensemble (i.e., to the closest cluster). This method was inspired by Gutierrez et al., [13] who used clustering in a forecasting problem. The technique used to cluster the historical dataset is the \(k\)-means [14]. This method is considered an optimization method because it seeks a partition that minimizes the sum of the distance between all the vectors in the same cluster (see for instance [15]). From now on, this method is mentioned as \(k\)-means and the corresponding metric as \(m_4\).
Prediction Methods
Once the best \(N_a\) analog have been identified, by means of one of the metrics described in the previous section, the prediction of the meteorological variable at time \(t\) can then be made. This is accomplished by means of the observations values (\(O_{t_i}\), with \(i=1,2,\ldots,N_a\)) at time steps matching the analogs (see Figure 1). The predicted value is then the average of these observation values, as given by Equation [6]. \[ P_t = \frac{1}{N_a}\sum_{i = 1}^{N_a} O_{t_i}. \label{prev1}\] Equation [6] needs to be adjusted when the Normalized Monache (\(m_2\)) or Cosine (\(m_2\)) metrics are used to obtain the analog ensemble. This is because in these cases what is looked at are trends and not exact equal numerical values, and so there might be a difference between the value of a meteorological variable at time \(t'\) and the desired value. Equation [6] thus becomes Equation [7], where \(\delta_{tt_i} = F_t-A_{t_i}\) accounts for the scale difference between the value of the variable in the analog and in the forecast. \[ P_t = \frac{1}{N_a}\sum_{i = 1}^{N_a} (O_{t_i} + \delta_{tt_i}). \label{prev2}\]
To improve the accuracy of the prediction, it is tempting to use data coming from various weather stations as predictors, instead of data coming from just one station. This raises the problem of how to treat this additional data. This problem was solved in two different ways, which were both used in this paper to determine which method is more adequate to handle data coming from various stations.
The first approach is the dependent stations method. This considers the stations to be nothing more than additional predictor variables, and as such computes analogs across all stations at once every time. That it, the observation at time \(t'\) is deemed to be an analog of the weather at time \(t\) if, and only if, the weather at all stations at time \(t'\) is close to the weather at all stations at time \(t\).
A second approach is the independent stations variant, in which the metric is calculated at each station independently from the other. The prediction is then made using the mean of the analogs from all the stations. Compared to the first approach, each station now forms a disjoint set of data in which analogs are searched separately. Then, weights are assigned to each stations to form the final set of analogs; for instance, with two independent stations, 90% of analogs may come from the study of the data from one station and the remaining 10% will come from the study of the data from the other station. With \(\alpha\) representing the weight of analogs from predictor station 1 and \(\beta=1-\alpha\) standing for the weight of analogs from predictor station 2, the predicted value will be given by Equation [8]. \[ P_t = \frac{1}{N_a}\left(\sum_{i=1}^{\alpha N_a}O_{t_{1i}} + \sum_{j=1}^{\beta N_a}O_{t_{2j}}\right) \label{eq:inde}\] where \(O_{t_{1i}}\) and \(O_{t_{2i}}\) are the observations that match the analogs from the predictors station 1 and 2.
Error Assessment
Measuring the errors of predictions against truth values (the values effectively registered by weather stations) is of paramount importance in order to assess the performance of the prediction methods.
As shown by Chai and Draxler [16], assessing a model accuracy is best done using various metrics. Three metrics are especially useful when trying to assess the performance of a forecasting model. The simplest of those metrics is the Bias, given by Equation [9].
\[ \mathrm{Bias} = \frac{1}{n} \sum_{i=1}^n (x_i - y_i), \label{bias}\]
where \(n\) is the number of predictions, \(x_i\) is a prediction and \(y_i\) is the corresponding truth value. As its name suggests, the Bias measures the bias of the model, which is simply the average error compared to the truth. However, it does not really show the behavior of the error. It is useful to determine if the model makes predictions that are lower or higher than the truth, but it is not enough in itself to really know how well the model performs. It only shows the systematic error of the model.
Thus, complementary to the Bias, the Root Mean-Squared Error (RMSE) is also used and corresponds to Equation [10]. \[ \mathrm{RMSE} = \sqrt{\frac{1}{n} \sum_{i=1}^n (y_i - x_i)^2}. \label{rmse}\] The RMSE is useful because the squared terms give a higher weight to higher errors. Thus, the RMSE will be higher if the model makes predictions which are far from the truth, even if these erroneous predictions are few in number.
To complement the Bias and RMSE metrics, the Standard Deviation of the Error (SDE) may also be considered. The SDE simply corresponds to Equation [11]. \[ \mathrm{SDE} = \sqrt{ \mathrm{RMSE}^2- \mathrm{Bias}^2}. \label{eq:sde}\] Considering the Bias as a basic indicator of the systematic error in a prediction, then the SDE is the equivalent indicator of the random error.
Finally, another useful metric, whose usage alongside the RMSE metric is recommended by Chai and Draxler [16], is the Mean Absolute Error (MAE) as presented in Equation [12]. \[ \mathrm{MAE} = \frac{1}{n} \sum_{i=1}^n |y_i - x_i|. \label{mae}\] Basically, the MAE metric computes an average distance to the truth, in absolute value. In turn, the Bias, whose expression is similar to the MAE minus the distance modulus, simply computes the average error in a way that allows for positive and negative errors to cancel each other. Therefore, the MAE gives a somewhat more truthful assessment of the average distance to the truth.
A low Bias and high MAE means that the model is not really accurate, but that its predictions are sometimes higher than the truth, and sometimes lower. Thus, taking the MAE into consideration is necessary to really understand how the error is distributed in the forecast, since it also shows systematic error, but this time in terms of absolute distance.
Computational Experiments
In this section the AnEn method enriched with the new similarity metrics, prediction methods and error assessment tools laid out previously, is put to the test, using real-world meteorological data.
Meteorological Datasets
Testing was done using the data from meteorological stations located on the coast of the state of Virginia, USA. These stations were used because their observations are freely available from the United States National Data Buoy Center [17]. The location of the stations is shown in Figure 2.
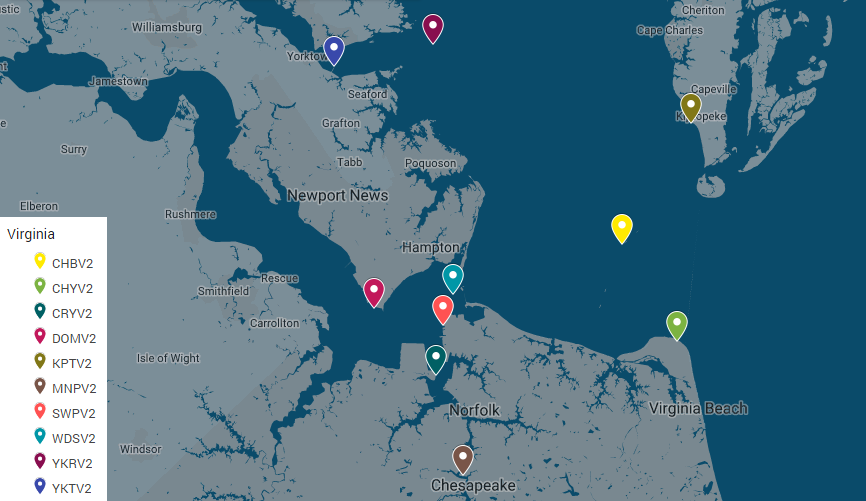
The data extends from the years 2012 to 2018. The data from the years 2012 to 2016 (training period) was kept as an historical database, and the aim of the experiment was to predict (reconstruct) the data from 2017 to 2018 (prediction/reconstruction period), at one station. The stations data was resampled by time-integration to match a sampling period of 6 minutes. These stations monitor 6 different meteorological variables: pressure (PRES), air temperature (ATMP), water temperature (WTMP), wind speed (WSPD), gust speed (GST) and wind direction (WDIR). Often, time series are not complete, data is missing for periods whose length may be short (hours) or long (months).
The idea was therefore to hindcast: at one station where only the meteorological data from 2012 to 2016 (training period) was known, the goal was to reconstruct, for that station, the data from 2017 to 2018 (prediction period), using other stations (predictors), where data for the full range of 2012 to 2018 was known. Based on the AnEn procedure illustrated in Figure 1, the data from 2012 to 2016 at the predicted station is the observed dataset whilst the data at all other stations between 2012 to 2018 is the historical dataset (comprised of multiple time series); also, the training and prediction periods correspond to intervals 2012 to 2016, and 2017 to 2018, respectively.
The main advantage of this setup is that it makes easy to evaluate the model accuracy, because one can compare the estimates obtained with the AnEn method with the real values. It is important to stress, however, that the data collected by stations every six minutes over a period of 7 years is huge, an so it would be very time consuming to sequentially process all the records in the historical dataset. Instead, the problem was simplified to predict the weather between 10 am and noon, using analogs of the weather for that specific time period. This greatly reduced computing time, while still providing data from different years and different seasons, thus covering very different weather patterns.
Tests Results
The results of the computational tests performed in the context of this work can be divided into two parts. In a first study, the importance of the choice of stations was assessed, to find how important choosing the right stations to hindcast the values at another station is. Then, since it is also possible to assign weights to stations, the importance of choosing the right weight was also studied. In both studies all the four metrics were applied to obtain the analog ensemble. All the tests where performed with a half time window \(k=20\), which corresponds to a time window of four hours in length (2 hours before the forecast, and two hours after), and a dimension of the analog ensemble of \(N_a = 25\).
The numerical results next presented and discussed were produced by a computational application developed in R [18] and executed in a Linux system of an HPC cluster located at CeDRI/IPB.
Assessment of the Predictor Station
As already stated, the first study aimed to evaluate how important is the choice of the predictor stations. To evaluate this, the gust speed (GST) data for the ykt station (YKTV2 in Figure 2) between the years 2017 and 2018 was reconstructed using the value of GST at three different pairs of stations.
Table 2 contains results (errors for different metrics used to find analogs) for an AnEn hindcast whose predictor was based solely on the mnp station (MNPV2 in Figure 2).
| Metric | Bias (\(m/s\)) | RMSE (\(m/s\)) | MAE (\(m/s\)) | ||
|---|---|---|---|---|---|
| \(m_1\) | 0.51 | 1.98 | 1.48 | ||
| \(m_2\) | 0.38 | 2.05 | 1.54 | ||
| \(m_3\) | 0.37 | 2.03 | 1.53 | ||
| \(m_4\) | 0.39 | 1.93 | 1.44 |
Figure 3 shows the positioning of the results in Table 2, also including the standard deviation (SDE) of each metric. The figure shows the same information present in Table 2 but in a visual form, taking advantage of the relation between RMSE, Bias and SDE in Equation [11]. By representing the Bias and SDE as coordinates, the RMSE becomes the distance to the origin. If the Bias is assumed as a zero-order measure of systematic error, then SDE is a measure of the random error. Hence, Figure 3 gives insight on the nature of the prediction error.
| Metric | Station 1 | Station 2 | Bias (\(m/s\)) | RMSE (\(m/s\)) | MAE (\(m/s\)) |
|---|---|---|---|---|---|
| \(m_1\) | dom | ykr | 0.95 | 2.34 | 1.75 |
| \(m_1\) | dom | mnp | 0.94 | 2.34 | 1.74 |
| \(m_1\) | wds | mnp | 0.24 | 1.75 | 1.33 |
| \(m_2\) | dom | ykr | 0.26 | 1.79 | 1.36 |
| \(m_2\) | dom | mnp | 0.68 | 2.01 | 1.52 |
| \(m_2\) | wds | mnp | 0.49 | 1.83 | 1.43 |
| \(m_3\) | dom | ykr | 0.43 | 1.81 | 1.37 |
| \(m_3\) | dom | mnp | 0.87 | 2.12 | 1.61 |
| \(m_3\) | wds | mnp | 0.73 | 1.94 | 1.51 |
| \(m_4\) | dom | ykr | 0.30 | 1.63 | 1.22 |
| \(m_4\) | dom | mnp | 0.43 | 1.85 | 1.38 |
| \(m_4\) | wds | mnp | 0.24 | 1.69 | 1.28 |
Table 3 shows results on extending the AnEn method to include a second station as a predictor. Pairs were made of stations mnp, dom, ykr and wds to assess results consistency across different pairs. Figure 4 shows the corresponding positioning of the results, again including the SDE metric.
Compared to this extension, the results in Table 2 and Figure 3 show less error and less SDE for the \(k\)-means (\(m_4\)) metric, while retaining similar Bias to the Cosine (\(m_3\)) and the Normalized (\(m_2\)) metric. As the main source of error is due to the SDE, the error in the predictions is not due to a systematic offset of the AnEn techniques employed. This is in line with the results from Table 3, where the \(k\)-means method consistently shows better performance. The simple application of the Monache metric (\(m_1\)) yielded higher Bias (which is also consistent with the results in Table 3). Normalizing the Monache metric shows overall improvements in the Bias and RMSE, though more evident in the results from Table 3. It is only for the \(<\)wds, mnp \(>\) pair of predictors that the Monache metric shows a superior performance, though the \(k\)-means metric still has lower RMSE and MAE.
Comparing results from Table 2 and Table 3, using mnp alone as predictor is worse than using mnp and either dom or wds for the \(k\)-means (\(m_4\)) and Normalized Monache (\(m_2\)) metrics. For the Cosine (\(m_3\)) and Monache (\(m_1\))metrics, it is clearly better to use both wds and mnp instead of mnp alone for hindcasting. However, for these metrics, it is better to use mnp alone rather than both dom and mnp.
Comparing the pure Monache metric (\(m_1\)) with the Normalized one (\(m_2\)), the results in Table 3 show that the latter leads to Bias and RMSE reduction. The only predictor pair where this was not observed was \(<\) wds, mnp \(>\); yet, the difference was not meaningful as it corresponds to 4% of higher RMSE. The cosine metric (\(m_3\)) behavior resembles the Normalized metric, though with degraded performances in the error metrics. This similarity was expected as both methods look solely for similar relative patterns in the time series.
As it can be seen in Table 3 and Figure 4, \(k\)-means (\(m_4\)) behave in the same way as Normalized Monache (\(m_2\)) and Cosine (\(m_3\)), which implies that clusterization employs a similar idea as these two methods. Results, however, are noticeably better.
These results show a rift between the methods: while \(k\)-means (\(m_4\)), Cosine (\(m_3\)) and Normalized Monache (\(m_2\)) all give results following the same trend, Monache’s results go in another direction. There is, however, a rational explanation for this behavior: Monache looks for analogs by minimizing the distance between the value of the target variable at time \(t\) (when the prediction is made) and at time \(t'\) (the analog). The other methods, however, disregard this distance. Instead, they look for a similar evolution of the weather during the time window. As such, the results implies that at the station dom weather follows a similar pattern as the station ykt, but because of the different location, meteorological values are not the same. This difference in value disturbs the Monache metric, but not the others, who look at the underlying weather patterns.
All methods, however, give their worse results with the \(<\)dom, mnp \(>\) pair, and always by a clear margin, while the \(<\)wds, mnp \(>\) pair performs well in all cases. This suggests that wds is a much better station to predict the weather at ykt compared to dom, and that ykr is a very good predictor station too, since it is able to offset the inaccuracies caused by the use of dom as predictor (except in the case of the Monache method, since Monache gives a great emphasis on numerical distance between values). Overall, the \(<\)mnp , wds \(>\) pair is the one giving the lower RMSE overall across all methods.
Figure 4 shows a trend where the error decreases mainly due to improvements in the Bias (hence systematic error) rather than the SDE. Moreover, the \(<\)dom , mnp \(>\) pair of stations yield worse agreement due to higher Bias.
As expected, results are improved when using two stations, compared to using just one. However, the results for Monache and Cosine metrics suggest that the choice of stations is important to really have an accuracy gain.
Assessment of the Predictor Stations Weights
| Metric | \(\alpha\) | \(\beta\) | Bias (\(m/s\)) | RMSE (\(m/s\)) | MAE (\(m/s\)) |
|---|---|---|---|---|---|
| \(m_1\) | – | – | 0.24 | 1.75 | 1.33 |
| \(m_1\) | 0.1 | 0.9 | 0.52 | 1.95 | 1.45 |
| \(m_1\) | 0.5 | 0.5 | 0.40 | 1.78 | 1.33 |
| \(m_1\) | 0.9 | 0.1 | 0.27 | 1.74 | 1.31 |
| \(m_2\) | – | – | 0.49 | 1.83 | 1.43 |
| \(m_2\) | 0.1 | 0.9 | 0.61 | 1.99 | 1.55 |
| \(m_2\) | 0.5 | 0.5 | 0.54 | 1.87 | 1.45 |
| \(m_2\) | 0.9 | 0.1 | 0.49 | 1.83 | 1.42 |
| \(m_3\) | – | – | 0.73 | 1.94 | 1.51 |
| \(m_3\) | 0.1 | 0.9 | 0.05 | 1.92 | 1.49 |
| \(m_3\) | 0.5 | 0.5 | 0.24 | 1.95 | 1.51 |
| \(m_3\) | 0.9 | 0.1 | 0.05 | 1.93 | 1.50 |
| \(m_4\) | – | – | 0.24 | 1.69 | 1.28 |
| \(m_4\) | 0.1 | 0.9 | 1.22 | 2.56 | 1.95 |
| \(m_4\) | 0.5 | 0.5 | 0.50 | 2.16 | 1.66 |
| \(m_4\) | 0.9 | 0.1 | -0.25 | 2.10 | 1.65 |
Once the importance of using the correct stations is assessed, it becomes important to evaluate if weighting the contribution from each predictor station can improve on the accuracy of the weather prevision at the ykt station. It is also important to compare the two ways of combining information from the two predictor stations, described in the section 2.3. For this, the focus is kept on the \(<\)wds, mnp\(>\) pair, whose results gave the lowest RMSE overall in the previous test. The question is to determine if it is possible to improve these results even further by assigning weights to these stations.
To this aim, both the independent stations and the dependent stations variants were used. The former variant allows weights to be set for each individual station, while the latter does not (recall section 2.3). In accordance with the Equation [8], \(\alpha\) is the weight of predictor station wds and \(\beta\) is the weight of predictor station mnp. As a consequence, in Table 4, tests results showing "–" in the weight columns are tests ran with the dependent method, while tests with numerical values in the weight columns are tests ran with the independent method. The target variable was kept the same (GST), for ease of comparison with the previous results. All the results are in Table 4 and Figure 5.
Considering the results from Table 4 and looking at the stations independently, the Monache metric (\(m_1\)) yields the best results, but only if the weights are equal. However setting most weight on wds (\(\alpha\)) is better than doing it on mnp (\(\beta\)). The Normalized Monache metric (\(m_2\)), however, prefers to have the analogs looked across all the stations at once. The Cosine metric (\(m_3\)) shows no big difference between the dependent and independent methods. The independent method performs slightly better when maximal weight is assigned to one station. In agreement with previous results, it appears that independent \(k\)-means metric gives best results when wds has most of the weight. However, even then it performs clearly worse than dependent \(k\)-means.
Figure 5 does not show a clear trend, though it may be considered that improvements are mostly due to lower Bias instead of SDE. Moreover, there are no changes in the SDE when weights are swapped between predicting stations (e.g. 0.1/0.9 to 0.9/0.1), and for most methods there is no advantage in applying those weights. The exception is the \(k\)-means method (\(m_4\)), which is sensitive to the weights as Bias largely changes. The best results, however, may be obtained for the dependent stations, e.g. without weighting.
The Figure 6 presents the Taylor diagram [19] for the best case of each method. It is possible to see that in general the Normalized metric (\(m_2\)) gives the best results. Its proximity to the truth indicates a high correlation coefficient with it, a low SDE value and similar positions on the horizontal axis shows similar standard deviations - in other words, the prediction obtained by the Normalized metric is close to the truth. Predictions from the \(k\)-means (\(m_4\)) and Monache (\(m_1\)) metrics are very close to one another, and also close to the truth, with a high correlation coefficient and a low SDE value. However, they are closer to the origin on the horizontal axis, indicating that their standard deviation is lower than that of the truth. This implies these methods have troubles following the variations of GST accurately. In general Cosine (\(m_3\)) is the metric which performs the worst - its coefficient correlation with the truth is lower than in other methods, and the RMS distance to the truth is higher. However, it has the closest standard deviation to the truth, meaning the cosine method is the method which follows the variations of GST the most accurately.
Figure 7 shows the prediction with the different metrics jointly with the truth values. As expected, the forecast by the Normalized metrics is the closest to the truth. It is interesting to note that while the prevision by the Monache and \(k\)-means metrics behave similarly, they look rather different from one another. Cosine metric, as expected, is the farthest from the truth but displays a lot of variability.
Qualitatively the Cosine and Normalized metrics give a representation of the time series with higher fidelity, due to additional variance. Quantitatively, however, the additional variance introduces mismatches which result in poorer accuracy when compared to the \(k\)-means and Monache metrics.
Conclusion
In this work, meteorological data was predicted at one location based on multiple historical datasets from weather stations located in other places. In order to achieve this prediction, the Analog Ensemble method was applied and several variants were explored by changing the metric used to determine the analogs in the historical dataset. The prediction period was two years, based on a training period of four years of historical and observed time series.
From all these results, it appears that the choice of predictor stations, and how to weight them if a weighted approach is used, has a significant bearing on the hindcasting, and presumably forecasting, accuracy. The problem of selecting stations for hindcasting and forecasting purposes is a non-trivial one, and from these experiments, it would appear that the best way to make a viable selection is to test hindcasting on known data simply, to determine which are the stations most suited to forecasting and hindcasting purposes at the target location. The use of the \(k\)-means metrics leads to an improvement ranging from 3% to 30% of lower quadratic error when compared against the Monache metric. Increasing the predictors to two stations improved the performance of the hindcast, leading up to 16% of lower error, depending on the correlation between the predictor stations. These features show the kind of improvements which can be made on the existing AnEn method.
The results look very promising. However, it is necessary to optimize several parameters that have not yet been analyzed. Therefore, the number of clusters was left at a basic value. It is possible to tweak this value and see how to set this value for maximal accuracy, or even control the size of clusters. The \(k\)-means algorithm is also a reasonably basic clustering algorithm, and more accurate algorithms now exist. It would be interesting to look at their performances compared to the basic \(k\)-means in this case.
It is also possible to look at larger scales, both in terms of the number of variables, number of stations, or distance between stations. The study presented in this paper focused on a rather simple testing environment, with stations located all next to each other. As a next step, it seems logical to look at the performances under larger scales of the various approaches studied.
Finally, the potential of the Analog Ensemble method to predict the weather variables at a given location can be useful to develop models for the operational management of agricultural plantations highly dependent on the weather, using short and medium-range weather forecasts downscaled to the spatial scales representative of the agricultural plantations location.
Authors’ Information
Carlos Balsa studied numerical methods at the Universidade do Porto and at Institut National Polytechnique de Toulouse, where he received a Ph.D. in Computational Sciences and Applied Mathematics. Currently, he teaches mathematics at the Polytechnic Institute of Bragança and his research interests are the numerical and computational methods concerning fluid mechanics, heat transfer, and data mining.
C. Veiga Rodrigues holds a Diploma Course from the Von Karman Institute for Fluid Dynamics and a Ph.D. in Mechanical Engineering by University of Porto. He is currently an Engineer at Vestas Wind Systems A/S, working in data analytics and atmospheric flow modeling focusing wind energy power plants. Formerly, he was a researcher at Universidade do Porto, having worked in the coupling between numerical weather models and engineering flow solvers.
Isabel Lopes holds a Ph.D. in Information Systems and Technologies by Universidade do Minho. She is Adjunct Professor at the Instituto Politécnico de Bragança and a researcher with the Applied Management Research Unit (UNIAG) in the same institute. She is also a member of the ALGORITMI research center at Universidade do Minho, has more than 70 published papers, and belongs to several scientific journals’ editorial boards.
José Rufino holds a degree in Systems and Informatics Engineering by Universidade do Minho, and a PhD in Informatics by the same university. He currently works as Coordinator Professor at the Instituto Politécnico de Bragança, where he teaches computer engineering subjects and researches with the Research Centre in Digitalization and Intelligent Robotics (CeDRI) in high-performance and parallel computing, with a focus on scientific computing problems.
Authors’ Contributions
Carlos Balsa developed the new metrics and prediction methods presented in section 2, participated in the design of algorithms and its implementation in R, performed part of the tests presented in section 3, and wrote parts of all the sections of the manuscript.
C. Veiga Rodrigues imported and prepared the meteorological data sets used by the R code, validated the test results using the error assessment metrics presented in section 2.4, produced the graphs presented in section 3, and participated in the writing of all sections of the manuscript.
Isabel Lopes coordinated the writing of the manuscript and performed part of the tests presented in section 3.2.
José Rufino improved the computational performance of the R code by exploiting parallelization facilities of the R language, monitored the execution of the tests in the CeDRI HPC cluster, and participated in the writing of all sections of the manuscript.
Competing Interests
The authors declare that they have no competing interests.
Funding
No funding was received for this project.
References
[1] E. N. Lorenz, “Atmospheric Predictability as Revealed by Naturally Occurring Analogues,” Journal of the Atmospheric Sciences, vol. 26, no. 4, pp. 636–646, 1969, doi: 10.1175/1520-0469(1969)26<636:aparbn>2.0.co;2.
[2] H. M. V. D. Dool, “A New Look at Weather Forecasting through Analogues,” Monthly Weather Review, vol. 117, no. 10, pp. 2230–2247, 1989, doi: 10.1175/1520-0493(1989)117<2230:anlawf>2.0.co;2.
[3] H. M. V. D. Dool, “Searching for analogues, how long must we wait?” Tellus A: Dynamic Meteorology and Oceanography, vol. 46, no. 3, pp. 314–324, 1994, doi: 10.3402/tellusa.v46i3.15481.
[4] L. D. Monache, F. A. Eckel, D. L. Rife, B. Nagarajan, and K. Searight, “Probabilistic Weather Prediction with an Analog Ensemble,” Monthly Weather Review, vol. 141, no. 10, pp. 3498–3516, 2013, doi: 10.1175/mwr-d-12-00281.1.
[5] S. Alessandrini, L. D. Monache, S. Sperati, and J. N. Nissen, “A novel application of an analog ensemble for short-term wind power forecasting,” Renewable Energy, vol. 76, pp. 768–781, 2015, doi: 10.1016/j.renene.2014.11.061.
[6] L. D. Monache, T. Nipen, Y. Liu, G. Roux, and R. Stull, “Kalman filter and analog schemes to postprocess numerical weather predictions,” Monthly Weather Review, vol. 139, no. 11, pp. 3554–3570, 2011, doi: 10.1175/2011mwr3653.1.
[7] S. Alessandrini, L. D. Monache, S. Sperati, and G. Cervone, “An analog ensemble for short-term probabilistic solar power forecast,” Applied Energy, vol. 157, pp. 95–110, 2015, doi: 10.1016/j.apenergy.2015.08.011.
[8] S. Alessandrini, L. D. Monache, C. M. Rozoff, and W. E. Lewis, “Probabilistic prediction of tropical cyclone intensity with an analog ensemble,” Monthly Weather Review, vol. 146, no. 6, pp. 1723–1744, 2018, doi: 10.1175/mwr-d-17-0314.1.
[9] A. Chesneau, C. Balsa, C. V. Rodrigues, and I. M. Lopes, “Hindcasting with multistations using analog ensembles,” in CEUR workshop proceedings, 2019, vol. 2486, pp. 215–229.
[10] E. Vanvyve, L. D. Monache, A. J. Monaghan, and J. O. Pinto, “Wind resource estimates with an analog ensemble approach,” Renewable Energy, vol. 74, pp. 761–773, 2015, doi: 10.1016/j.renene.2014.08.060.
[11] National Center for Atmospheric Research. https://nar.ucar.edu
[12] K. Adachi, Matrix-based introduction to multivariate data analysis. Springer Singapore, 2016.
[13] J. M. Gutiérrez, A. S. Cofiño, R. Cano, and M. A. Rodrı́guez, “Clustering methods for statistical downscaling in short-range weather forecasts,” Monthly Weather Review, vol. 132, no. 9, pp. 2169–2183, 2004, doi: 10.1175/1520-0493(2004)132<2169:cmfsdi>2.0.co;2.
[14] J. MacQueen, “Some methods for classification and analysis of multivariate observations,” in Proceedings of the fifth berkeley symposium on mathematical statistics and probability, 1967, vol. 1, pp. 281–297.
[15] L. Eldén, Matrix methods in data mining and pattern recognition. Philadelphia, PA, USA: SIAM, 2007.
[16] T. Chai and R. R. Draxler, “Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature,” Geoscientific Model Development, vol. 7, no. 3, pp. 1247–1250, 2014, doi: 10.5194/gmd-7-1247-2014.
[17] National Data Buoy Center. https://www.ndbc.noaa.gov
[18] R Core Team, R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing; Vienna, Austria, 2017. http://www.r-project.org
[19] K. E. Taylor, “Summarizing multiple aspects of model performance in a single diagram,” Journal of Geophysical Research: Atmospheres, vol. 106, no. D7, pp. 7183–7192, 2001, doi: 10.1029/2000jd900719.
